夏晓光(loveJY)的博客

parent指针$u->v$,当且仅当$min_u=min_v+1$,而且v代表子串均为u子串后缀

显然所有节点沿着parent指针走都会走到初始节点

在parent树中,$子节点endpos \subset 父节点endpos$

然后我调了一下下,学了学zhq,谢谢zhq教我做人

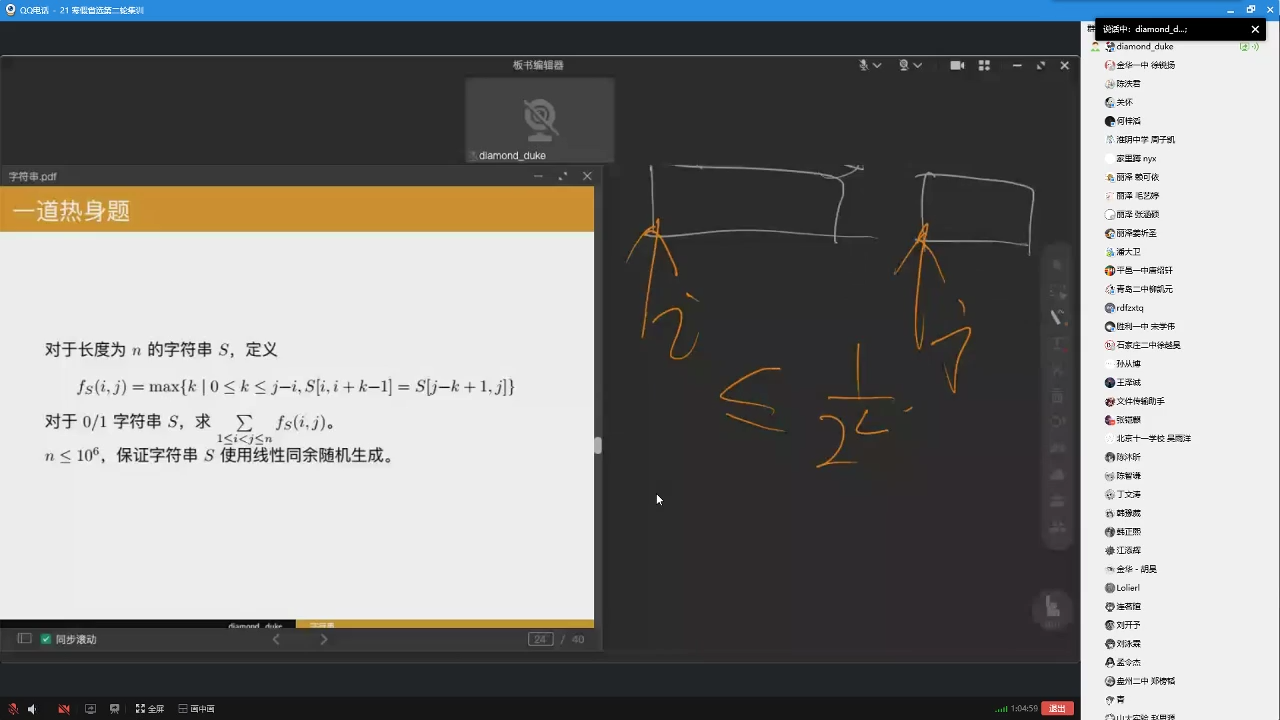
$f(S)$不超过$logn$

那...我们怎么关心他们啊

这样的串不超过$O(nlogn)$个,而且总长度也不会超过$O(nlogn)$(因为一个是另一个前缀)

枚举一个串T,然后看有多少串$border$,就是他

怎么把最长给去掉啊

注意到border的结构,对于一个串而言,

最长border的最长border是大串的次长border

也就是沿着这个串一直找一定能找到他的次长border

现在我们想计算出一个东西的权值(权重),然后加权乘上出现次数做掉

我们观察可以有:

!

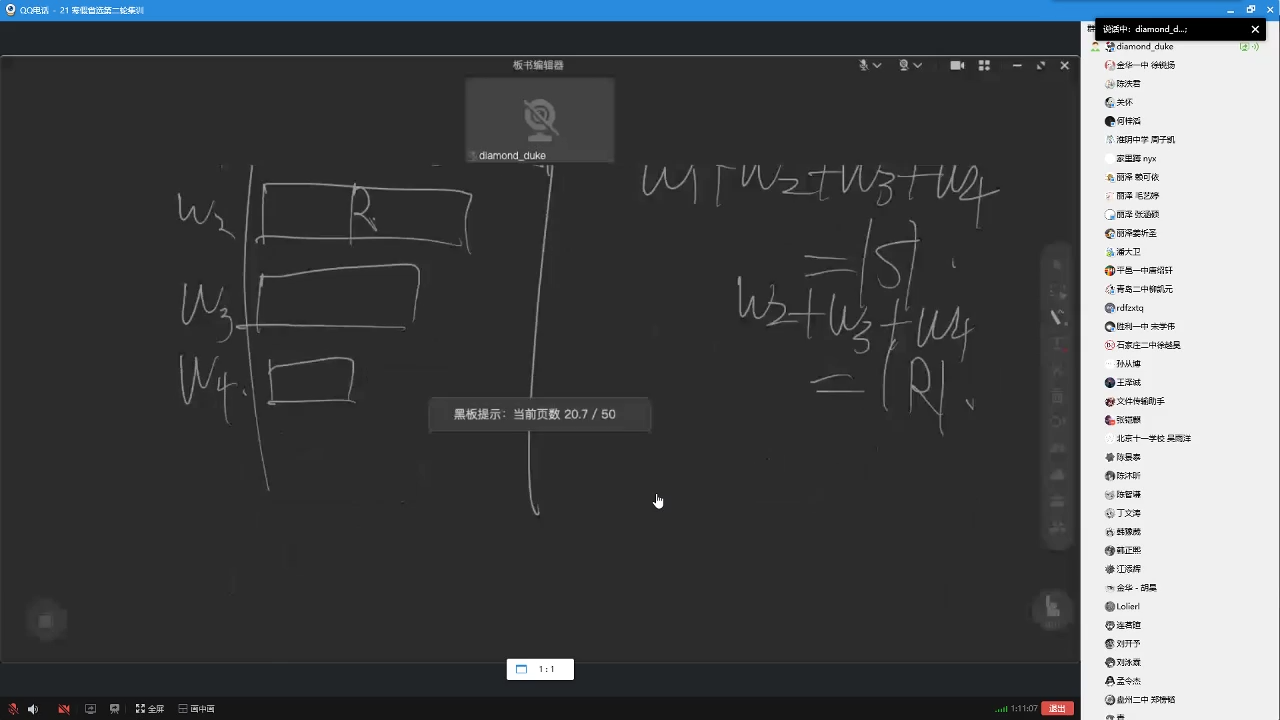所以我们令一个串的权值是$S-maxborder S$就做完了

考虑那个出现次数是什么,其实就是在大串中的出现次数$\binom{cnt_T}{2}$

这个出现次数不需要SAM,建立字典树插入每个位置所有长度为$logn$的串即可......

因为这个S不会很多,所以我们可以暴力求border,我们只对于所有最长的串求kmp,就能知道他们所有前缀的border的长度,相应就能知道所有的了!

这个复杂度$O(nlogn)$

首先有一个暴力的想法:

枚举一个节点endpos集合两个元素,相当于会对$l\leq i,r\leq j$的所有询问产生$max(len_u,ans_i)$的贡献,同时询问就变成了单点查询,按照R排序后树状数组首先取max即可

但是问题是第一步枚举两个元素太慢了...甚至可以达到$O(n^3)$

我们再仔细思考一下,对于一个endpos集合,观察这个式子,只有所有相邻的有用,其他一定不优

其次,我们如果有i,j属于同一个子树,那么这个i,j一定是不会再这个节点计算答案的

于是我们i,j分居不同的节点

同时根据相邻,我们知道如果启发式合并,插入一个数只记录他的前驱后继,那么这样的询问至多有$T(2nlogn)$个,所以就可了!

所以我们只需要在启发式合并的过程中产生询问即可

复杂度$O(nlog^2n)$,瓶颈在于回答询问和启发式合并....都是两个log

qwq我是除了$n^2$一点都不会

考虑1:k中那些点能成最优解

首先只有所有最小字符开头的串能成为最优解

然后我们增量一步,所有以最小字符+最小字符的串能成为最优解

假设$i<j$

我们考虑对于前k个字符,如果这两个后缀满足他们LCP是小于k-j的,那么就一定会在前k个字符不循环的情况下就比出来他更优,那么哪一个大留下哪一个

所以说考虑我们只保留了这样的元素,从$p_{k-1}$看,$p_{k}=p_{k-1}+s_k$,$s_k$是后缀k

同样要满足上述条件就是任意的都大于,

因此我们精妙的设计一下这个比较过程就是O(n)的

就是按照长度排序,然后两两求lcp即可,有一个后缀数组就搞定了

因为我们考虑对于$i<j<k$,如果i,j是合法的,那么如果i,k满足条件那么j,k就满足条件了!

所以我们具体维护方法就是排序之后先比较i,j合法比较j,k,如果i,k可以删掉i,再去比较$i,k$,否则删掉了k,在比较下一个就好了,其实就是类似双指针的过程,把所有合法的集合连边保留下来!

然后怎么求答案呢?暴力?

每次维护和查询好像是$O(|p_k|)$

然后我们要给他一个上界啊,否则就上天了...

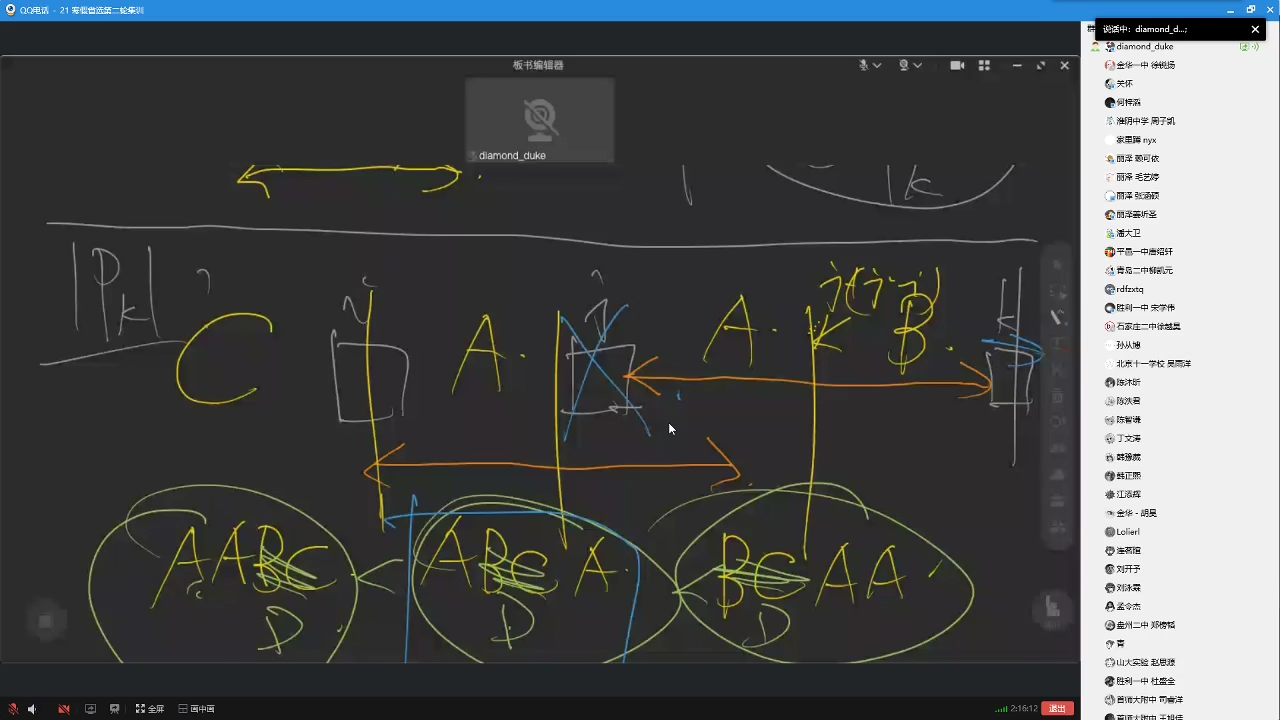
那,假设D为BC,你会发现,对于i,j以及$2j-i$,这三个后缀

就有无论D的字典序比i大还是比i小,j都不可能成为最优解!

所以我们就删掉了j!!

于是你会发现如果i和j相距太近就会导致这种情况出现,具体的,这个i和j的lcs不能跨过去啊

就是$j-i> k-j$,这个j才可能是合法的

所以有$k-i>2(k-j)$也就是说这个操作之后,至少要满足一倍的关系才能有一个合法的

所以这个上界就是$O(logk)$

更新答案?

然后现在就是比i这一后缀和j这一后缀谁大$LCP(s_i,s_j)$黄色部分和蓝色部分

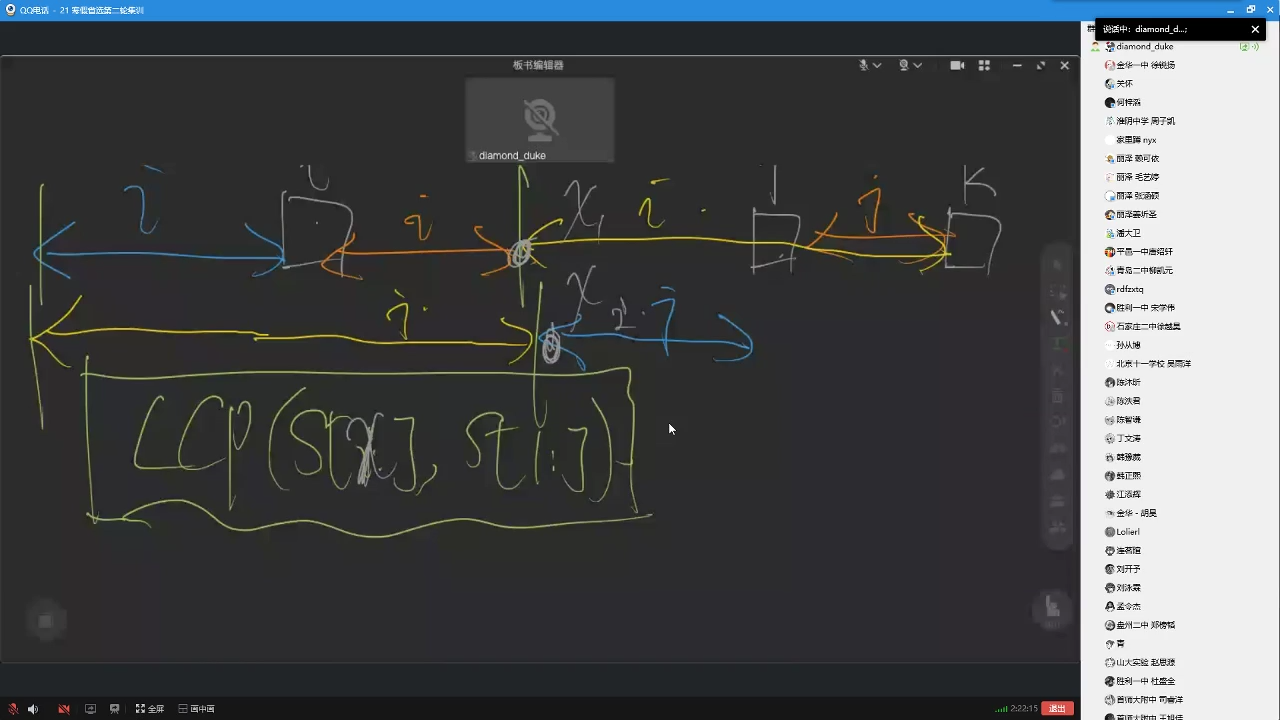
然后如果黄色的比出来了就停止,否则比下面的

这个比较过程就是O(n)的,类似数组求最小值,zhq教我的,谢谢zhq爷爷

扩展kmp...求下式

$lcp(s_x,s_{1~j})$

至于扩展kmp是什么我也没学会反正就后缀数组一下回答lcp也是$O(1)$的吧

复杂度是$O(n+\sum P_k)$

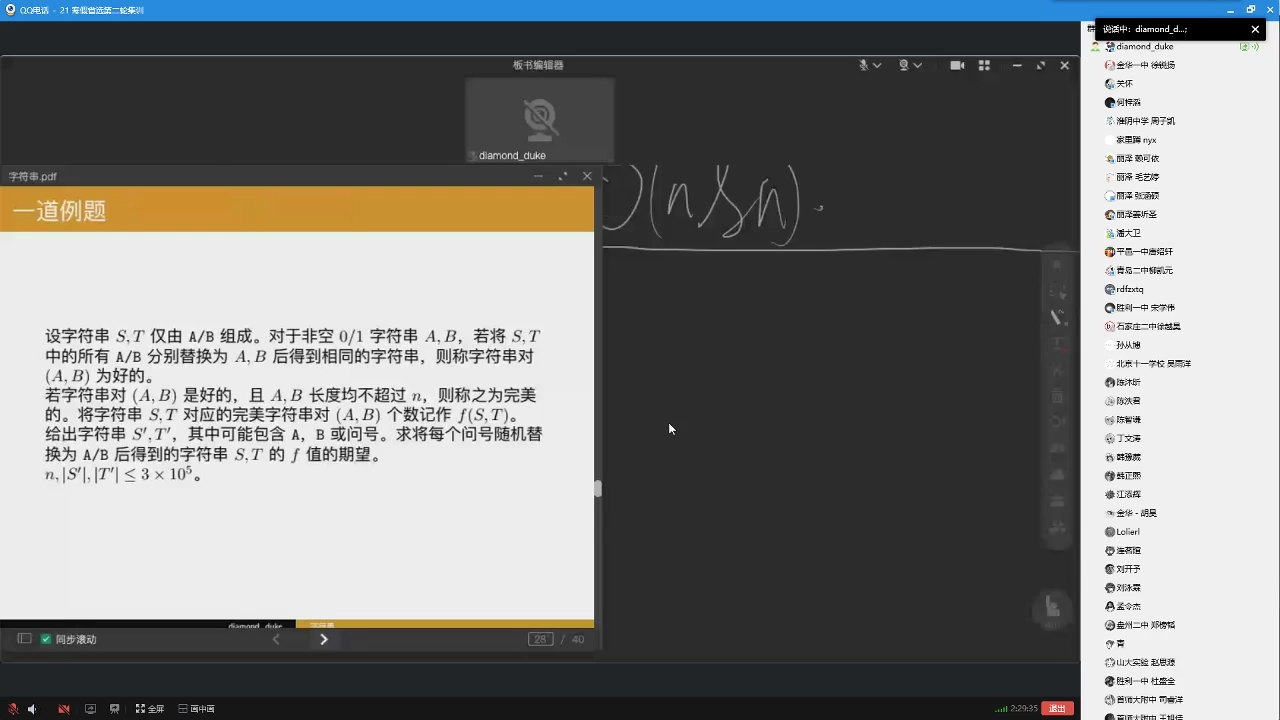
首先,如果S和T第一位或者最后一位相同,我们都可以一直删除

如果得到空串,那么a,b随便都是可以的

第二种情况,两端都是A对应B中间有一些字符如果$|A|<|B|$

那么A是B的border因为A和B的前x位和后x位都是一样的

于是我们会发现无论放a还是b,这个都是一样的,也就说$B=A^{\infty}$

A就是B的周期,同时对于borderx显然有y-x也是$period$

弱周期引理:

$x,y~ is~ period$

$x+y\leq |S|$

那么gcd(x,y)是$|S|$的整周期

还有一个

周期引理

$x+y\leq |S|+gcd(x,y)$

那么也有这个性质成立

又因为$gcd(x,y)=A$

$A=c^a,B=c^b$

那么答案就是

$\sum_{x=1}^n\sum_{y=1}^n2^{gcd(x,y)}[xlen=tlen]$

长度相同,等价统计有多少个A,或者B

然后$sax+sby=tax+tby$

$px=qy(pq互质)$

1. p=q=0

$Ans=\sum_{q=1}^{n}2^q(2*phi(n/q)-1)$

直接筛即可!$O(n+\sqrt n)$

2. p,q都不为0

那你就会发现x=qk,y=pk

就是$\displaystyle \sum_{k=1}^n[qk\leq n,pk\leq n]2^{gcd(pk,qk)}$

你会发现p,q互质就么了

就是$\sum_{k=1}^{m}2^{k}$

没有问号就处理完了,有问号怎么办

答案就是$\sum_{i=0}^{s_i}\sum_{j=0}^{t_i}\binom{s_i}{i}\binom{s_j}{j}F(sa-ta+i-j,sb-tb+s?-i-t?+j)$

枚举i-j

$\displaystyle \sum_{k=0}F(sa-ta+k,sb-tb+..-k)*\sum_i\sum_j[i-j=k]\binom{s?}{i}\binom{t?}{j}$

$\displaystyle \sum_{k=0}F(sa-ta+k,sb-tb+..-k)*\sum_i\sum_j[i+j'=k+T?]\binom{s?}{i}\binom{t?}{j}$

显然右边是一个组合恒等式,范德蒙德卷积

$\binom{s?+t?}{k}$

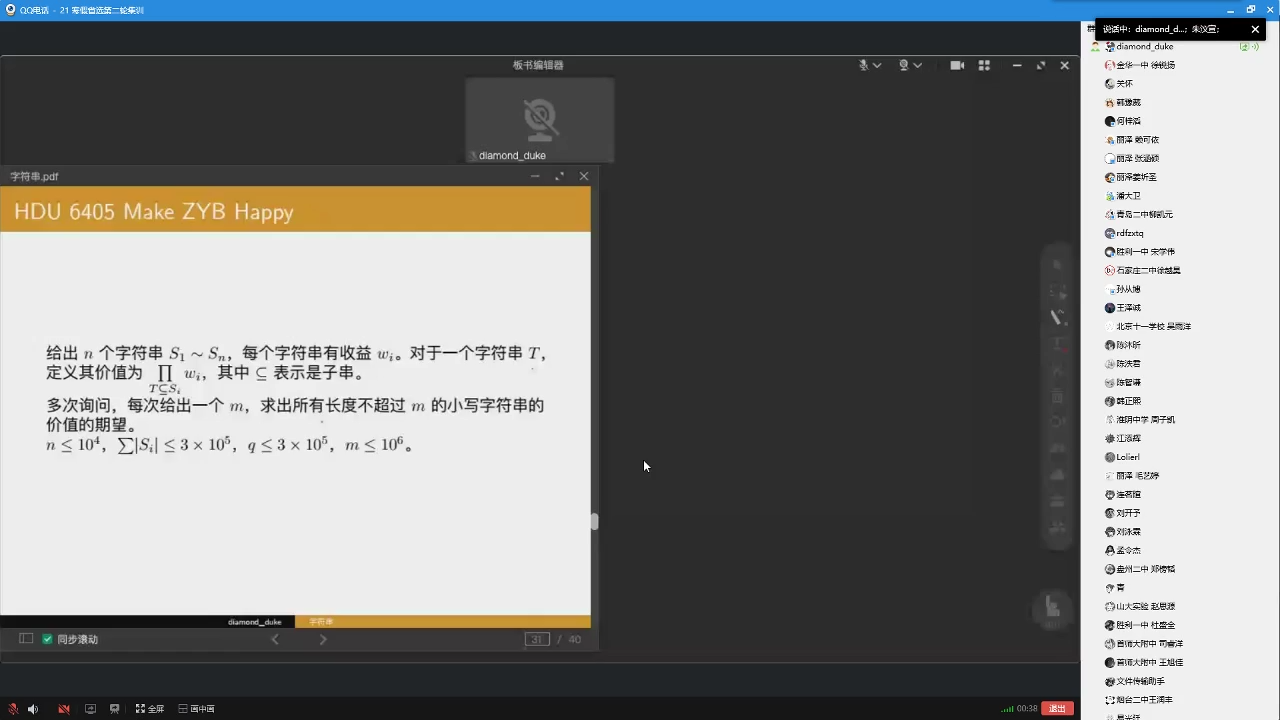
首先建立广义SAM,然后利用SAM的根号平衡可以求出所有点包含于哪些串同时乘起来他

然后答案就是对于某一个串而言他可能代表了多个c,我们求出每个节点答案就是整个的答案就好了

复杂度是啥啊

一个串,长度为$|S_i|=L$,我经过点数显然不超过是$O(L^2)$

同时因为我们不会经过重复的点,设m为总长度

就是长度为L的串,经过点数为$min(L^2,m)$

每个字符有贡献$min(L,\frac{m}{L})$

后式小于$\sqrt m$

所以总复杂度就是$O(m\sqrt m)$

那么也就是说我们很妙其实卡不满

然后直接统计每个点贡献就好了,注意这里写的是T是S的子集,所以很简单答案就是所有点的贡献$/26*26^2*26^3....$

根号做法还是很简单的...

每次先把所有点爬出来

然后拓扑dp一遍统计一下子树和就好了!就能知道每个子串在某个地方出现次数了

于是我们前i次得到的对应系数显然也可以维护,因为只是一个和吗,然后乘上每个串对应的出现次数得到即可

我们可以大工业题,用树剖解决这个sam的后缀树

然后对于每个前缀节点,相当于一个到根的路径加

维护这个点代表串的和即可,答案就是和*和...

所以我们直接修改即可,然后单点查询对应系数,乘上一些信息即可

树链剖分都可以解决,复杂度$O(nlog^2n)$,当然也可以全局平衡二叉树代替,复杂度是$O(nlogn)$

xqq扣了5个1,他特别懂

!

读入挺成问题的

我很是精通$n^2$

直接dp有决策单调性!?

g怎么快速求啊

当l=1的时候,怎对于任意r求出答案?

可以考虑扫描线过去?然后每次加入一个字符就能知道新的r端点个上次的区别,sam即可

对所有串建立trie,然后前第i层节点个数就是$g_{1,r}$

有$g_{1,r}$能不能求$g_{2,r}$?

我们把根节点第二层的trie合并即可!

那么不难发现一直合并下去就能知道所有$g_{r,r}$了!复杂度就是$O(nm\sum S)$

因为我么每一次递归下去都会少一个点,所以总合并复杂度就是深度m字符集大小

所有的$g_{l,r}$太多了...所以我们要想办法压下去

你会发现他能分成许多段,而每一段的值域只有$[1,m]$之间,所有断点$R_{l,k}$表示从l开始后k个值域相同

$R_{l,k}=\min_{l\leq r\leq n|g_{l,r}\geq k|}l$

$L_{r,k}$表示最大的l使得$l\leq r,g_{l,r}\geq k$

第一维为长度第二维为个数就有了O(nm)!

接下来怎么转移呢?

$f_l->f_r,g_{l,r}=k$

$f_l+\sum A_l(r-l)+pg+Br$

对于同样的r可以考虑k能够分段

$L_{r,k}\leq l\leq R_{r,k}->g_{l,r}=k+1$

如果左端点在这个范围内取就确实可以知道是k了

然后最大....QAQ

于是有老哥告诉我们有O1带修rmq!这是什么神仙操作啊!

有一个小trick?

我们只需要限制下界

假如说l实际上比这个小,那么此时我们转移系数更劣,所以肯定会被真正正确k用更大权值搞掉

而你发现只需要不让一些变优,即只限制下界没有上界即可

因此我们只需要一个前缀max即可

因此我们对于一个前缀,每一个l影响到的就是一个区间了

就相当于每次插入一条直线,然后询问某个点处的最大值

我们再对l扫描线,然后维护一堆直线和直线的凸包

用set维护支持插入删除即可

现在就是枚举一个l,然后转移需要枚举每个k进行查询复杂度$O(mn)$

首先不难算本质不同的子串数

然后考虑最长出现过的后缀有多长,相当于要找最大的l,使得$p_{l,j}$

是s的子串

我们要找对于j,所有$T_{l,j}$是S的子串

考虑所有字符串都要加$T_{j+1}$

如果不存在这么一个v,那么考虑这一段我们要变为$[l+1,j]$

$T_{l,j}\in u$

如果l+1之后长度不够了就要跳一步next!

这样就能求出$T_{l,j}$对应节点

因此双指针维护一下就能求出所有的最小l了

现在我们知道每个节点最多延展多少了

考虑每个点记录一个end的位置,这个位置作为j最少要延伸多久才不是j的位置

所以我们就能知道T建立sam之后,对于每个后缀节点都有一个限制,然后和代表长度取min来统计一下即可

具体实现就是两个自动机上一起匹配,当s匹配好了之后,长度可能不尽人意,于是我们再在t上跳匹配知道长度合法即可

最后线段树合并一下就能知道我们每一步能不能走了复杂度也就有保证了$O(TlogS)$

我很会$N^2$

优秀的拆分就是求所有平方串,这个题也有一步是优秀的拆分

我们求形如AA这样的串!

枚举A的长度L,然后每L个打一个标记,那么对于一个平方串一定会经过两个相邻的标记

然后做法就是考虑

$LCP(s_L,s_{2L})$

$LCS(s_L,s_{2L})$

如果他们的和大于这个间隔就是合法的

就能知道每个位置开始的答案了然后我们就能得到logn个区间就是O(nlogn)平方串,起始位置都是一个区间

然后考虑一个固定的循环节长度L

我们可以建出这样的图

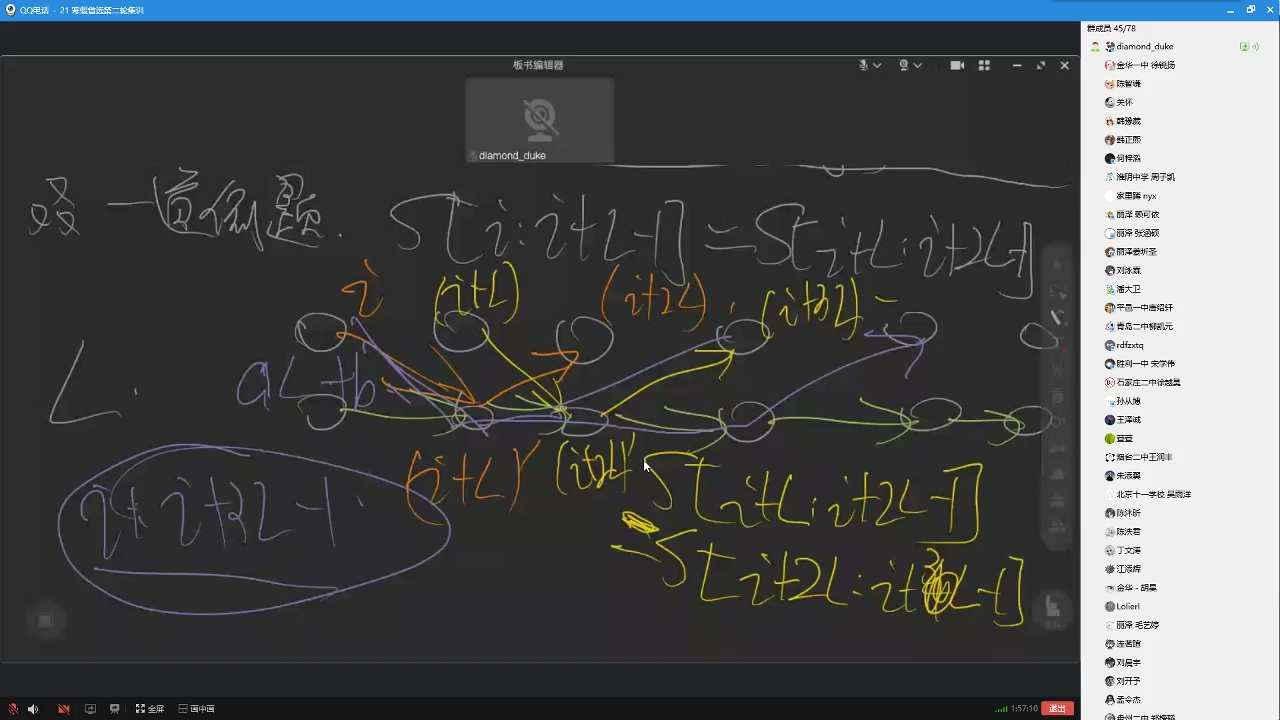
其中上面的点都是正常的点,下面都是辅助转移点

如果满足$S[i+L:i+2L-1]$相同,我们就把i+L'向i+2L'建边

这样我们就会发现把虚点相邻的连边即可最优化

但是现在边数太多了!!

我们考虑$S_{i,i+L-1}$是一个最小整循环节,那么大于他们的都不用管,这个位本原平方串

然后有一个结论就是本原平方串个数不超过$O(nlogn)$

对于一个左端点固定的一些平方串

如果$2l_i\geq l_{i+1}$,根据周期引理,有一个$gcd(l_i,l_{i+1})$的循环节

那就告诉我们这两个串都不本原就都干掉即可

然后我们就只需要连接那些本原平方串对应的边即可

复杂度$O(nlogn)$,拓扑排序转移即可

三类边是1. $i-a>(i+L)'$

2. $i+L'-0>i,i+L-0>i+2L$

本原平方串就是如果我已经知道x和x+L是本原的就有他的倍数的都不是,要筛掉他们,因此所有没有筛掉的都是本原的

$N^2$可以暴力跳fail建立相等的信息....

然后有道叫萌萌哒的题

首先每一个限制可以拆成$(u,v,2^k)$,表示u出发$2^k$等于v出发$2^k$

所以对于每一个k,我们都维护一个并查集,如果在一层中u,v unit起来就说明从u出发$2^k$=v出发$2^k$,所以我们每次把那些边拆掉push到下一层即可

那你就会发现每一次向下一层就只有n条边

这题也一样,把u,v,k拆成$u,v,k-1$和$u+2^{k-1},v+...,2^{k-1}$

那只需要把所有一个颜色的连起来即可

时间复杂度也确实是$O(nlogn)$

乘上一个并查集复杂度...

计数好像也能做??

如果fail树和某个树有公共边

然后这道题v代表串s_v,u代表串s_u

说明s_v是s_u+c的后缀,周期就是1,那么$s_u$就是ccccccc

然后如果这个公共边中存在一个点度数为3,就是根

问题是我们没有这样的点,只有一个链

如果没有其余边就都是a

否则就会有一个其余的点,在trie上连了出去

那么这个点一定是aaaaaab

然后我把这个点不断跳fail,你会发现一直都跳不到这个链上,就是aaaaab->aaaab->aab->b

唉?b的下一步就跳到链上了,所以就是根了!

找到根之后我们重复之前那倒题的做法即可!

这题有点眼熟啊

好像ybtoj原题啊就是CF那个吧

我们先建立sam,然后考虑合并的答案

就是对于一个节点u,他一定是合并不同的儿子时得到了可能转移的方案

对于他的前缀,一定是他代表的某一个后缀在之前出现过

那直接对于每一个endpos判一下就好了,就知道能不能转移了

注意如果我们不能转移要把父亲中长度最短的那个继承下来,所以我们不断的沿着sam把dp向下push即可

所以总复杂度就是$O(logn)$