夏晓光(loveJY)的博客

仍要向下扎根,向上结果

首页 归档 标签 关于 友链

织田信奈的生成函数进阶篇

2021-01-04 35 min read # 織田信奈の野望 # 生成函数

本篇集中于EGF和OGF的应用于试题选讲

前置知识(其实只是作者复习):

eF(x)=1+F(x)+F(x)22!+F(x)33!.....e^F(x)=1+F(x)+\frac{F(x)^2}{2!}+\frac{F(x)^3}{3!}.....

复合函数求导

f(g(x))′=f′(g(x))g′(x)f(g(x))'=f'(g(x))g'(x)

即11−xv\frac{1}{1-x^v}

等价于f(x)=1xf(x)=\frac{1}{x}

与1−xv1-x^v的复合

一阶导数为(1−xv)′∗−vxv−1(1-x^v)'*-vx^{v-1}

导数乘积运算法则:

(f∗g)′=f′g+f∗g′(f*g)'=f'g+f*g'

除法运算法则为:

(f/g)′=f′g−fg′g2(f/g)'=\frac{f'g-fg'}{g^2}

5748 集合划分计数

答案等于∑i=0nStri\sum_{i=0}^nStr_i

即第一类斯特林数一行的和

这个数叫做贝尔数

bell(n)即将n个球放入m个本质相同的盒子方案数

显然对于答案的OGF,我们有枚举多少个集合,然后在这些集合中放入球的方案数,每多出一个就卷一下

G(x)=∑i=0∞Fi(x)i!G(x)=\sum_{i=0}^{\infty}\frac{F^i(x)}{i!}

故答案为G(x)=eF(x)−1G(x)=e^{F(x)-1}

其中F(x)是这个集合的指数生成函数,如果是普通生成函数,由于集合的无序性我们必然算重

5401 [CTS2019]珍珠

CTS的题

考虑朴素的dp做法

我们是计数染色方案,使得每种染色方案能两两配对的达到m个

dpi,j,kdp_{i,j,k}表示前i个球,我们已经考虑前j种颜色,当前有k个pair的方案数

转移一次转移一种颜色,即我们枚举这种颜色用掉多少球,然后除以用掉数量的阶乘

最后乘上n!就好了

n4n^4运气极佳有28分呢

这个显然是没法写成生成函数的,考虑优化

观察数据范围,有m=0的部分

不难发现此时答案就是DnD^n....汗

也有m=1的部分,此时我们要计算所有数都不相同的方案,用总方案-都不相同方案,也很简单,都不相同等价于能形成全排列即D!

m=2,容斥一下,这提示我们利用容斥解决本题

至少能选m个行,等价于恰好有0个不行,这个不好求,可以变为至多m个不行-至多m-1个不行+?*至多m-2个不行

于是打开题解,我们有

∑c=1D⌊cntc2⌋>=m\sum_{c=1}^D\lfloor\frac{cnt_c}{2}\rfloor>=m

拆开这个符号等价转换一下

∑c=1Dcntcmod  2≤n−2m\sum_{c=1}^Dcnt_c\mod2\leq n-2m

也就是说我们可以特判了

设oddkodd_k为cntccnt_c恰好有k个为奇数的方案数

∑i=0n−2moddi\sum_{i=0}^{n-2m}odd_i

考虑容斥,至少有k个的方案数是fkf_k

那么fk=∑j=kn(jk)oddjf_k=\sum_{j=k}^n\binom{j}{k}odd_j

oddk=∑i=kn(−1)i−k(ik)fiodd_k=\sum_{i=k}^n(-1)^{i-k}\binom{i}{k}f_{i}

显然我们这个组合数拆开后就是卷积而已,考虑怎么计算这个fif_i

奇数?生成函数即可

显然使用EGF,我们有

fk=(Dk)n![xn](ex−ex2)ke(D−k)xf_k=\binom{D}{k}n![x^n](\frac{e^x-e^x}{2})^ke^{(D-k)x}

对于右边二项式展开,随手化简有

fk=(Dk)n!2k∑j=0k(kj)(−1)k−j[xn]e(D−2k−2j)xf_k=\binom{D}{k}\frac{n!}{2^k}\sum_{j=0}^k \binom{k}{j}(-1)^{k-j}[x^n]e^{(D-2k-2j)x}

eax=EGF1,a,a2,a3...e^ax=EGF{1,a,a^2,a^3...}

于是带入上式

fk=(Dk)n!2k∑j=0k(kj)(−1)k−j(D−2k−2j)nn!f_k=\binom{D}{k}\frac{n!}{2^k}\sum_{j=0}^k \binom{k}{j}(-1)^{k-j}\frac{(D-2k-2j)^n}{n!}

于是说这个就是卷积的形式了,构造两个多项式卷起来即可

时间复杂度?n-2m显然小于这个D吧,所以是DlogDDlogD

djq有dlogdndlog_dn orzdjq贴贴

具体的,第一个式子,我们变成

∑i=0n−k(−1)ii!fi+k∗(i+k)!=k!∗oddk\sum_{i=0}^{n-k}\frac{(-1)^i}{i!}f_{i+k}*(i+k)!=k!*odd_k

然后对于第二个翻转我们设好的数组,然后进行卷积,得到的第三个数组再翻转回来,然后再乘上阶乘

第二个式子是

∑j+i=k1j!(−1)i(D−2i)ni!=fk∗(D−k)!∗2kD!\sum_{j+i=k}\frac{1}{j!}\frac{(-1)^i(D-2i)^n}{i!}=\frac{f_k*(D-k)!*2^k}{D!} 


#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int MAXN = 6e5 + 7;
const int P = 998244353;
const int G1 = 3;
const int G2 = (P + 1) / 3;
int D, n, m;
ll F[MAXN], G[MAXN], H[MAXN];
ll fac[MAXN], ifac[MAXN];
inline ll ksm(ll x, ll y) {
	ll ans = 1;
	while(y) {
		if(y & 1)ans = ans * x % P;
		x = x * x % P;
		y >>= 1;
	}
	return ans;
}

int L, len, R[MAXN];

inline void init() {
	int n = D;
	fac[0] = 1;
	for(int i = 1; i <= n; ++i)fac[i] = fac[i - 1] * i % P;
	ifac[n] = ksm(fac[n], P - 2);
	for(int i = n - 1; i >= 1; --i)ifac[i] = ifac[i + 1] * (i + 1) % P;
	ifac[0] = 1;
	return ;
}

inline void init1(int n) {
	L = 0;
	len = 1;
	while(len < 2 * n)len <<= 1, ++L;
	for(int i = 0; i < len; ++i)R[i] = (R[i >> 1] >> 1) | ((i & 1) << (L - 1));
	return ;
}

inline void NTT(ll *F, int len, int typ) {
	for(int i = 1; i < len; ++i)if(i < R[i])swap(F[i], F[R[i]]);
	for(int mid = 1; mid < len; mid <<= 1) {
		ll wn = ksm(typ == 1 ? G1 : G2, (P - 1) / (mid << 1));
		for(int j = 0; j < len; j += (mid << 1)) {
			ll w = 1;
			for(int k = 0; k < mid; ++k, w = w * wn % P) {
				ll x = F[j + k], y = F[j + k + mid] * w % P;
				F[j + k] = (x + y) % P;
				F[j + k + mid] = (x + P - y) % P;
			}
		}
	}
	if(typ == -1) {
		ll inv = ksm(len, P - 2);
		for(int i = 0; i < len; ++i)F[i] = F[i] * inv % P;
	}
}

inline void out(ll *F) {
	for(int i = 0; i <= 2 * n; ++i)printf("%lld ", F[i]);
	puts("\n");
	return ;
}

inline void solve1() {
	for(int i = 0; i < D + 1; ++i) {
		G[i] = ifac[i];
	}
	for(int i = 0; i < D + 1; ++i) {
		if(i & 1)H[i] = P - 1;
		else H[i] = 1;
		H[i] = H[i] * ksm((D - 2 * i + P) % P, n) % P;
		H[i] = H[i] * ifac[i] % P;
	}
	init1(D + 1);
	NTT(G, len, 1);
	NTT(H, len, 1);
	for(int i = 0; i < len; ++i)G[i] = G[i] * H[i] % P;
	NTT(G, len, -1);
	for(int i = 0; i < D + 1; ++i)F[i] = G[i] * ifac[D - i] % P * ksm(ksm(2, i), P - 2) % P * fac[D] % P;
	for(int i = 0; i < len; ++i)H[i] = G[i] = 0;
	return ;
}

inline void solve2() {
	for(int i = 0; i < D + 1; ++i)F[i] = F[i] * fac[i] % P;
	reverse(F, F + D + 1);
	for(int i = 0; i < D + 1; ++i) {
		if(i & 1)G[i] = P - 1;
		else G[i] = 1;
		G[i] = G[i] * ifac[i] % P;
	}
	init1(D + 1);
	NTT(F, len, 1);
	NTT(G, len, 1);
	for(int i = 0; i < len; ++i)G[i] = G[i] * F[i] % P;
	NTT(G, len, -1);
	for(int i = D + 1; i < len; ++i)G[i] = 0;
	reverse(G, G + D + 1);
	for(int i = 0; i < D + 1; ++i)G[i] = G[i] * ifac[i] % P;
}

inline void zhqwq() {
	for(int i = 0; i < 6; ++i)F[i] = 1;
	for(int i = 0; i < 6; ++i)G[i] = 1;
	init1(6);
	NTT(G, len, 1);
	NTT(F, len, 1);
	for(int i = 0; i < len; ++i)F[i] = F[i] * G[i] % P;
	NTT(F, len, -1);
	for(int i = 0; i < len; ++i)printf("%lld ", F[i]);
	puts("\n");
}

int main() {
	scanf("%d%d%d", &D, &n, &m);
	if(n < 2 * m) {
		puts("0");
		return 0;
	}
	if(D <= n - 2 * m) {
		printf("%lld\n", ksm(D, n));
		return 0;
	}
	init();
	solve1();//解决F数组
	solve2();
	ll ans = 0;
	for(int i = 0; i <= n - 2 * m; ++i)ans = (ans + G[i]) % P;
	printf("%lld\n", ans);
	return 0;
}

P5293 [HNOI2019]白兔之舞

宽度为3的网格图不同路径长度计数?

L<=1e5L<=1e5

我们考虑dp,先忽视题目让我们求什么

对于dpi,jdp_{i,j}表示走到列i行j的点的方案数

转移考虑前缀和优化,对于每一行处理前缀和数组gjg_j

于是我们有

dpi,j=∑gk∗wk,jdp_{i,j}=\sum g_{k}*w_{k,j}

这个dp的复杂度很低是nL

但是我们要记录长度,才能回答询问....,即第二维modkmod k意义下的路径长度qaq

dpi,j,k=∑gl,k−1wl,jdp_{i,j,k}=\sum{g_{l,k-1}w_{l,j}}

哎?k这一维好像是一层一层转移的啊?

所以我们可以通过改变w来倍增优化这个dp,复杂度就是O(Lpolylog)O(Lpoly log)

对于N=1N=1

我们有个很好的性质,就是这个走路的方案数是隔板法

具体的,用i步,我们的方案数就是

(ni)∗w[1][1]i\binom{n}{i}*w[1][1]^i

答案也就不言而喻了

正解要单位根反演和MTT,就不学了

P3784 [SDOI2017] 遗忘的集合

∏j=1m(11−xvi)=F(x)\prod_{j=1}^m(\frac{1}{1-x^{{v_i}}})=F(x)

给出这F,问v_i,还要求字典序最小....

我连n=5都不会

正解

我们这个式子显然不优美,变成

∏i=1n(11−xvi)ai=F\prod_{i=1}^n(\frac{1}{1-x^{v_i}})^{a_i}=F

也就是说我们直接枚举取值,去看aia_i看看这个是0还是1

同时取负对数(PH)

∑i≥1ailn(1−xvi)=−ln⁡F\sum_{i\geq 1}a_iln(1-x^{v_i})=-\ln F

里面那个直接展开

∑i≥1ai∑j≥1xijj=ln⁡F\sum_{i\geq 1}a_i\sum_{j\geq 1}\frac{x^{ij}}{j}=\ln F

这个式子就差不许多,我们变形一下,枚举这个T=ij

∑T≥1xT∑d∣TaddT=ln⁡F\sum_{T\geq 1}x^T\sum_{d|T}a_d\frac{d}{T}=\ln F

有对应项系数相等!!然后我们就可以直接莫比乌斯反演了:

aT∗T=∑d∣Tln⁡F(d)dμ(Td)a_T*T=\sum_{d|T}\ln F(d)d \mu(\frac{T}{d})

就做完啦!

时间和代码复杂度瓶颈在于MTT,这种题一般msl

P4548 [CTSC2006]歌唱王国

要做这个题,我们先引入第三类生成函数:概率型生成函数

对于某个随机变量X∈ZX\in Z

构造数列an{a_n}满足ai=Pr(X==i)a_i=Pr(X==i)

我们就有这个数列的生成函数

∑i=0nPr(x==i)xi\sum_{i=0}^nPr(x==i)x^i

为随机变量X的PGF

这个定义下的生成函数巨大的好处是什么呢?

你考虑他的一阶导数

有∑i=0nPr(x==i)i∗xi−1\sum_{i=0}^nPr(x==i)i*x^{i-1}

系数和就是期望,根据期望的线性性有下式

Var(x)=E((x−E(x))2)=E(x2)−E(x)2Var(x)=E((x-E(x))^2)=E(x^2)-E(x)^2

平方的期望-期望的平方

这个方差也是一样的可以用EGF表示呢

相当于方差前一项就是二阶导数+一阶导数

因为i∗(i−1)=i2i*(i-1)=i^2

注意三阶导数是E(x3)E(x^3)

例题

有一个随机变量z,然后每次有pkp_k概率让z加上k,并且z=z+kz=z+k

求min(z,x)min(z,x)的期望,答案mod 998244353

k<=100,kx<=5e7,n<=1e9k<=100,kx<=5e7,n<=1e9

写出答案的PGF,显然其n次方的前x项就能计算出答案

具体的P(x)=∑i=1kpixiP(x)=\sum_{i=1}^kp_ix^i

PnP^n前x项的概率他们直接算期望,后面的用1-前面的项概率和然后权值是x直接算期望,不是循环卷积注意要多项式快速幂

怎么加速这个过程?注意,我们的P(x)P(x)只有100项()

(Pn+1(y))′=(n+1)Pn(y)(P′(y))(P^{n+1}(y))'=(n+1)P^{n}(y)(P'(y))

这个牛逼的东西叫做链式法则,即复合函数求导的一个嵌套法则

显然就是g(f(x))′g(f(x))',其中g(x)=xn+1,f(x)=P(y)g(x)=x^{n+1},f(x)=P(y)

然后我们分出一项n,进行导数乘法运算,又能有

(Pn+1(y))′=Pn(y)(P′(y))+(Pn(y))′P(y)(P^{n+1}(y))'=P^{n}(y)(P'(y))+(P^n(y))'P(y)

上下做差

nPn(y)(P(y))′=(Pn(y))′P(y)nP^n(y)(P(y))'=(P^n(y))'P(y)

也就是说,我们先求出(Pn(y))′(P^n(y))'的一项,然后考虑积分得到Pn(y)P^n(y)的下一项

然后通过积分的结果和Pn(y)(P(y))′P^n(y)(P(y))'卷一下,直接暴力这一步Ok刷表对于后面贡献,然后这样求出来的d+1项系数就是右边多项式的系数

然后对于前d-k+1项系数,用多项式除法计算第d+1项答案,具体的

∑j=0kPj∗(Pk−jn)′\sum_{j=0}^kP_j*(P^n_{k-j})'

所以我们直接把j=0提出来减去j>0的值*p_0的逆元qwq

回到本题

F(x)为答案的生成函数,即到i位置停下来的概率

G(x)为到i位置没有停下来的概率

于是我们考虑G(x)怎么求,相当于G(x)+F(x)=1+x∗G(x)G(x)+F(x)=1+x*G(x)

相当于每一种情况加上任意一个字符,转移到停下来或者没有停下来的概率,同时特判边界1

设aia_i为每个位置是否为border的bool数组

然后我们钦点G转移到停下来,就有

G(x)∗(1mx)L=∑i=0nai(1mx)L−iF(x)G(x)*(\frac{1}{m}x)^L=\sum_{i=0}^{n}a_i(\frac{1}{m}x)^{L-i}F(x)

这个式子刻画了什么呢?左边显然是随意的一个式子后面接上答案式子的概率,然后停了下来

然鹅,我们想,这个可能会提前停下来,就算重了,但是只能是利用了他的所有borderborder 算重了,所以相当于接上了一个border就停了,剩下的长度又白接了

然后我们把1式求导,然后E(x)=F′(1)E(x)=F'(1)就有

F′(1)+G′(1)=G′(1)+G(1)F'(1)+G'(1)=G'(1)+G(1)

F′(1)=G(1)F'(1)=G(1)

然后我们把1带入第二个式子

G(1)=∑i=1LaiF(1)(1m)L−iG(1)=\sum_{i=1}^La_iF(1)(\frac{1}{m})^{L-i}

F(1)=1F(1)=1

G(1)=∑i=1Lai∗miG(1)=\sum_{i=1}^La_i*m^i

做完了

难度在于kmp

code:


//不用多项式算法的生成函数
#include<bits/stdc++.h>
#define int long long
const int P = 1e4;
const int MAXN = 1e6;
int n, t;
int a[MAXN], f[MAXN], fail[MAXN];

signed main() {
	scanf("%lld", &n);
	n %= P;
	scanf("%lld", &t);
	for(int i = 1, len; i <= t; ++i) {
		scanf("%lld", &len);
		for(int i = 1; i <= len; ++i)scanf("%lld", &a[i]);
		for(int i = 1; i <= len; ++i) {
			fail[i] = 0;
			f[i] = 0;
		}
		int ans = 0;
		fail[1] = 0;
		for(int i = 2, p = 0; i <= len; ++i) {
			while(p && a[p + 1] != a[i])p = fail[p];//如果p还没有跳没了,而且还必须要跳的时候,就跳一步
			if(a[p + 1] == a[i])//如果下一个字符能够成功匹配,就匹配上,然后再让这个p++
				fail[i] = p + 1, ++p;
		}
		for(int i = len; i ; i = fail[i]) {
			f[i] = 1;
		}
		for(int i = 1, tmp = n; i <= len; ++i) {
			if(f[i])ans = (ans + tmp) % P;
			tmp = tmp * n % P;
		}
		printf("%04lld\n", ans);
	}
	return 0;
}

P3706 [SDOI2017]硬币游戏

再做没时间复习多项式了

首先有一道好像一模一样的题:[JSOI2009]有趣的游戏

那道题的套路就是可怕的n6n^6高斯消元

我们可以直接对于所有串建出AC自动机,然后跑fail匹配就能知道每个点的匹配点,以及后面加上一个字符会跳到哪个点

然后我们对于所有点有一个状态f[i]表示i节点代表的串在S中经过的期望次数

转移我们有f(1)=1,同时其他除了end节点直接向外转移了

不难发现在关键点停下来就是经过次数的期望,因为你只会经过一次

同时关键点不能向外转移

但是这不是唯一的状态设计方法

fif_i表示节点i经过的概率

然后我们考虑和之前一样的可以使用向后继转移的方式,同时end节点不能向外走

然鹅此时建立的是n元齐次方程组,是会存在全0解的qwq

于是: 所有的end节点概率之和为1

所以这个做法也就等价于反推,从停止的状态来反推其他所有的概率

然后对于本题我们可以PGF了

上述问题瓶颈在于我们用了大量没用的状态,而只有n个状态有用

所以直接考虑把所有不合法的状态压成一个状态,然后写一个超级复杂的转移方程即可

因为对于一个S,考虑S+xiS+x_i同时len(xi)=mlen(x_i)=m

那么如果xix_i存在一个长度为a的前缀能够让xjx_j的一个后缀匹配的话,就有12m−a\frac{1}{2^{m-a}}的概率,在没能接上i这个完整字符串的时候中途结束了!

更具体的,加入我们现在的混乱没用态S,正在接上一个字符串i,但是由于border理论,我们可能中途易辙而导致这个停下来,最后成了字符串j

同时我们也不难得到转移方程

xi+∑j=1n∑a=1m[prea,xi=sufa,xj]12m−axj=12mSx_i+\sum_{j=1}^n\sum_{a=1}^m[pre_{a,x_i}=suf_{a,x_j}]\frac{1}{2^{m -a}}x_j=\frac{1}{2^m}S

这样就有n个方程,最后再加上所有字符串概率和为1这个方程高消即可

PGF的做法和这个类似,前半部分抄袭歌唱王国,然后得到第一个式子后,后半部分用border中途易辙的性质强行搞出第二个式子,素质极差

P7275 计树

这个题很牛逼啊

首先原问题可以变成一个把1到n1到n排好序的序列划分成若干段然后用凯莱定理拼起来的答案

差不多就是∏xinr−2\prod x_i n^{r-2}那个东西

然后我们发现这样玩命计重

先变成生成函数的卷积的形式

F(x)=∑i=2ni∗n∗xiF(x)=\sum_{i=2}^{n} i*n*x^i

ans=(∑i=1∞F(x)i)ans=(\sum_{i=1}^{\infty}F(x)^i)

这个东西乘上一个容斥系数就能算出真实方案了

马耀华爷爷告诉我们一种很不错的方式容斥

图片在EA 练习赛2

(一不小心就截多了QAQ)

也就是说,我们只看一个真实方案,然后抓住他为什么被算重的原因,也就是他被算重的虚假方案的形式

相当于我们把这个树划分成了不同的几段,然后让这些段按照相同的样子拼起来,然后加起来系数就不太对

所以说我们要把每个虚假方案加权削细一点!也就是加上一个容斥系数,这个容斥系数满足求和等于1

也就是(∑i=1∞G(i)i)[xn]=[n>1](\sum_{i=1}^{\infty} G(i)^i)[x^n]=[n>1]

又因为所有方案本质相同,所以我们一起算一起削也是一样的!

F(x)=∑i=2nG(x)[xi]∗i∗n∗xiF(x)=\sum_{i=2}^{n} G(x)[x^i]*i*n*x^i

问题是这个容斥系数具体是啥啊QAQ

你会发现这个相当于

11−G(x)−1=11−x−1−x\frac{1}{1-G(x)}-1=\frac{1}{1-x}-1-x

于是就做完了!

G(x)=x21−x+x2G(x)=\frac{x^2}{1-x+x^2}

直接exp这个F即可qwq

P6694 强迫症

首先如果我们能求出一个n个点的circle连成的方案数才能够带权计数

这个可以考虑dp

fif_{i}表示i个点的答案

枚举一号点连接的最小的是什么

然后我们就可以把问题变成1−>i1->i这些点组成的子问题1

然后i号点可以向后面连边,就是i−>ni->n共n−i+1n-i+1个点的答案

然后fn=fn−1+∑i=2nfi∗fn−i+1f_{n}=f_{n-1}+\sum_{i=2}^{n}f_{i}*f_{n-i+1}

其中前一项是不连接i的方案,但是这个是错的,因为我们钦定了1和i连边,但是方案数却没有体现...就是显然会有1->i不连边的方案

那么我们总会发现,其实1−>i1->i这条边连边和这条边不连边方案是一样的!因为他们都不会影响其他边的连接,在点集1−>i1->i中

但是后面我们选择的方案数决定了这个强制连上了

所以是fi/2f_{i}/2

fn=fn−1+12∑i=2nfi∗fn−i+1f_{n}=f_{n-1}+\frac{1}{2}\sum_{i=2}^{n}f_{i}*f_{n-i+1}

这个式子需要处理才能做啊,因为这显然是自卷积不好分治FFT的

先把卷积卷积变成从和为n的,因为和小于等于n的都可以添加x来做啊,这个做法可以想办法换元

fn=fn−1+12∑i=1n−1fi+1fn−if_n=f_{n-1}+\frac{1}{2}\sum_{i=1}^{n-1}f_{i+1}f_{n-i}

后面卷积系数和为2,所以

gn=fn+1g_n=f_{n+1}

gn−1=gn−2+12∑i=1n−1gign−i−1g_{n-1}=g_{n-2}+\frac{1}{2}\sum_{i=1}^{n-1}g_ig_{n-i-1}

gn=gn−1+12∑i=1ngign−ig_n=g_{n-1}+\frac{1}{2}\sum_{i=1}^ng_ig_{n-i}

这个式子我们加入这个0项

gn=gn−1+12∑i=0ngign−i−12gng_n=g_{n-1}+\frac{1}{2}\sum_{i=0}^ng_ig_{n-i}-\frac{1}{2}g_n

因为说g0=f1=1g_0=f_1=1

gn=23gn−1+13∑i=0ngign−ig_n=\frac{2}{3}g_{n-1}+\frac{1}{3}\sum_{i=0}^ng_ig_{n-i}

发现是

G(x)=23xG(x)+13G(x)2G(x)=\frac{2}{3}xG(x)+\frac{1}{3}G(x)^2

然后发现这个式子常数项不对,注意我们递推式转生成函数的时候要修正常数项

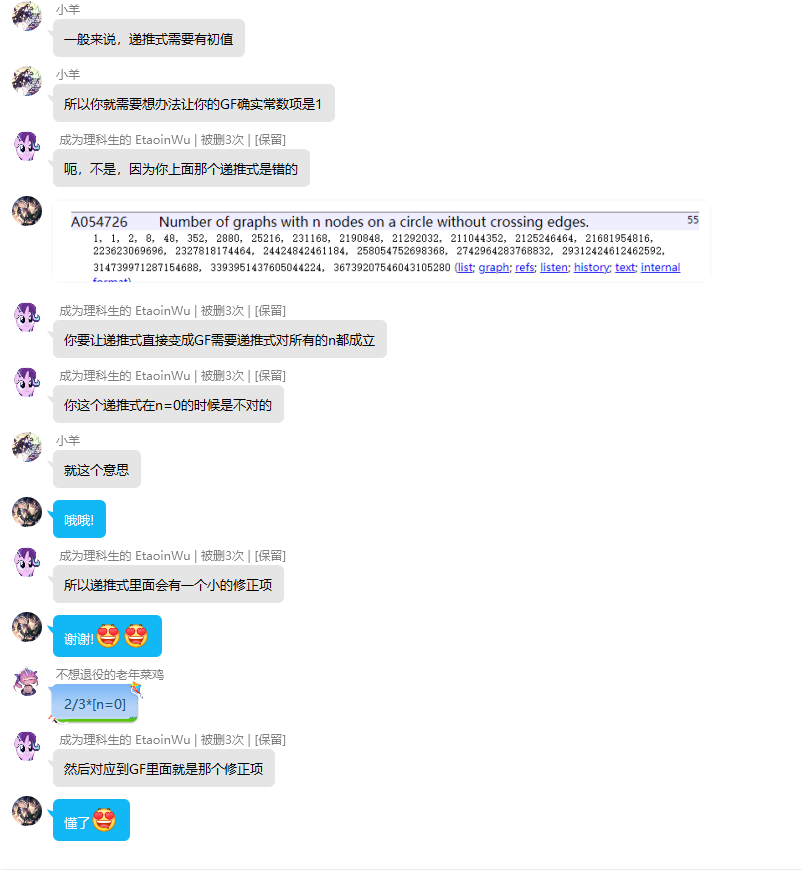
所以对于这个式子求解可以得到F的生成函数通项形式

有个根号下二次函数,可以通过多项式exp完成???

题解有一个很妙的做法

f=4x2−12x+1f=4x^2-12x+1

F=f1/2F=f^{1/2}

F′f=12Ff′F'f=\frac{1}{2}Ff'

可以自己推一下,链式法则啊

这个啥意思呢?我们要求这个F的每一项系数,那么可以通过左右的每一项系数相等来进行一点点计算得出他的系数!

我们甚至可以推广这个做法:

F=fkF=f^{k}

求F,乘积后求导

F′f=kFf′F'f=kFf'

F(x)=∑i=0aixiF(x)=\sum_{i=0}a_ix^i

F′(x)=∑i=0ai+1(i+1)xiF'(x)=\sum_{i=0}a_{i+1}(i+1)x^{i}

如果其中f多项式次数不多,那么我们可以打开其中的卷积项

然后你会发现,其中前i项的信息我们已经知道了,那么第i+1项的信息可以直接由前i项的信息推导出来,因为只有F'中有第i+1项,这样做一遍就是O(f次数的)O(f次数的)

这里具体的就不实现了....

最后我们推出答案式子,考虑对于每条边算贡献

1hn∑i=1n∑j=i+1naiajhj−i+1hn−(j−i−1)4\frac{1}{h_n}\sum_{i=1}^n\sum_{j=i+1}^na_ia_j\frac{h_{j-i+1}h_{n-(j-i-1)}}{4}

注意此时我们是可以成环的,所以那个乘积项会把i,j两个点都算两遍

后面那个东西如果我们写成

∑j=1i−1ajhi−j+1∗hn−(i−j−1)4\sum_{j=1}^{i-1}a_j\frac{h_{i-j+1}*h_{n-(i-j-1)}}{4}

fi=hi+1∗hn−i+1f_i=h_{i+1}*h_{n-i+1}

就是aj∗fi−ja_j*f_{i-j}

就完全卷积了

code:

#include<bits/stdc++.h>
#define ll long long
const int P = 998244353;
const int MAXN = 5e5 + 7;
using namespace std;
const int G1 = 3;
const int G0 = 332748118;
int n, L, len, R[MAXN];
ll h[MAXN], f[MAXN], A[MAXN], B[MAXN], a[MAXN];

inline ll ksm(ll x, ll y) {
	ll ans = 1;
	while(y) {
		if(y & 1)ans = ans * x % P;
		x = x * x % P;
		y >>= 1;
	}
	return ans;
}

inline void add(ll &x, ll y) {
	x += y;
	if(x >= P)x -= P;
}

inline void init() {
	h[0] = 1;
	h[1] = -6;
	for(int i = 1; i <= n; ++i)
		h[i + 1] = ((12 * i - 6) * h[i] % P - (4 * i - 8) * h[i - 1] % P) % P * ksm(i + 1, P - 2) % P;
	for(int i = 0; i <= n; ++i)h[i] = (P - h[i]) % P;
	h[0] += 3;
	h[0] %= P;
	h[1] -= 2;
	h[1] %= P;
	ll tmp = ksm(2, P - 2);
	for(int i = 0; i <= n; ++i) {
		h[i] = 1ll * h[i] * tmp % P;
	}
	for(int i = 1; i <= n; ++i) {
		f[i] = h[i] * h[n - i] % P, f[i] %= P;
	}
	return;
}

inline void init2() {
	len = 1;
	L = 0;
	while(len < 2 * n)len <<= 1, ++L;
	for(int i = 0; i < len; ++i)R[i] = (R[i >> 1] >> 1) | ((i & 1) << (L - 1));
	return ;
}

inline void NTT(ll *F, int typ, int len) {
	for(int i = 0; i < len; ++i)if(i < R[i])swap(F[i], F[R[i]]);
	for(int mid = 1; mid < len; mid <<= 1) {
		ll wn = ksm(typ == 1 ? G1 : G0, (P - 1) / (mid << 1));
		for(int j = 0; j < len; j += (mid << 1)) {
			ll w = 1;
			for(int k = 0; k < mid; ++k, w = w * wn % P) {
				ll x = F[j + k], y = 1ll * F[j + k + mid] * w % P;
				F[j + k] = (x + y) % P;
				F[j + k + mid] = (x - y + P) % P;
			}
		}
	}
	if(typ == -1) {
		ll iv = ksm(len, P - 2);
		for(int i = 0; i <= len; ++i) {
			F[i] = 1ll * F[i] * iv % P;
		}
	}
	return;
}

int main() {
	scanf("%d", &n);
	for(int i = 1; i <= n; ++i) {
		scanf("%d", &a[i]);
	}
	init();//预处理f
	for(int i = 1; i < n; ++i) {
		A[i] = a[i];
	}
	for(int i = 1; i < n; ++i) {
		B[i] = f[i];
	}//强行卷一下吧
	init2();
	NTT(A, 1, len);
	NTT(B, 1, len);
	for(int i = 0; i < len; ++i)A[i] = A[i] * B[i] % P;
	NTT(A, -1, len);
	ll ans = 0;
	for(int i = 0; i <= n; ++i) {
		add(ans, a[i]*A[i] % P);
	}
	h[n - 1] = (h[n - 1] + P) % P;
	ans = ans * ksm(4 * h[n - 1] % P, P - 2) % P;
	printf("%lld", ans);
	return 0;
}
Powered by Gridea RSS