T1

结论:最优不可能走超过两步解决

如果有多个线段,我们可以用调整法证明其不会更优秀qwq

即选取其中的一个折点,从起点或终点向他连边,并且删掉他上面原来的路径

你会发现这样也可能有限制,就是边经过了整点,这样我们再从另一个方向向整点连一个向量过去,重复上述过程,但是我们一直这样做下去一定不会有多余整点在线上了(相当于gcd)

有一个结论就是对于每一个凸多边形完全包含他的凸多边形,周长一定小于里面那个多边形

第一个做法就是对于每个x找到最靠近这个方向的两个向量,检查这个向量是否能满足加起来等于他

你会发现直线的方程相当于带入的坐标点(x,y)点积上直线方向向量(m,n)

首先把(m,n)翻转变为(-m,n), $-mx+ny=c$,然后gcd下m,n使其为1

然后我们有对于c=1,也就是在(-m,n)方向上投影为1的向量组成的直线,上面的格点一定就是转折点

可以证明一下,如果有一个点在c=2处取到,那么我们证明c=2夹角中一定要有一个整点

根据exgcd的通解的公式,我们有对于一个$(m,n)$方向上固定走l就有第二个解

$x'=x+n,y'=y+m$吗...

所以说我们有c=1平行于这个(n,m)啊,所以说对于c=2根据中位线那个交段的长度一定大于l,所以其中一定有一个交点

所以说我们把(0,0)按照c=1那个直线对称到另一侧,利用将军饮马找到最小的交点处,然后用通解公式找到其上下第一个格点即可qwq

时间复杂度$O(log)$

T2

考虑到过两个端点就能做了$n^3$

我们枚举两个端点,然后这个就是我们的答案,然后直接判断

其余的一定过一个端点,此时大概率是相切被卡住,而且是在两个线段中被卡住

对于一个两个端点在向量中的,如果我把他的端点向起点和终点方向移动,答案一定会变得更短,直到被卡主

我们过一个点的线段有一些旋转角度

把这个点能看到的线段全部写出来,我们会发现转动这个角度,这个角度和答案函数是凸函数....

证明?yjz口胡我,他说你可以插值插一下,就是凸的

所以我们可以三分这个角度

但是你会发现我们有看到很多线段,两个线段上是Olog三分的

所以说只需要在线段上two pointers枚举线段就好了,这一步是O(n^2log)的

T3

我们把所有值写在一个圆环上(因为是模意义下的),然后你会发现所有点和点之间连的线段最优下是不可能包含的,异向线段是不可能相交的

就比如| > | > 我们不可能那2匹配3,1匹配4

同时一个有向线段是不可能把整个环覆盖一周的还超过的,可以调整这个线段的起点上个线段的终点来成为一个负的线段

既然不会相交,我们就可以选取一个点,满足两边都是向外的,然后从哪个点剖开,从这个点向两侧直接贪心匹配

最后我们直接枚举这个点,然后从这个点两侧贪心匹配即可qwq

T4

无向图

无限长的黑白相间路径等价于走到一个奇环黑白相间而且最后一个点是重复的

这个是充要条件

点双连通分量一定存在一条u->v->w的简单路径

证明可以用网络流

无向图的话,枚举三个点,v从起点连进去流量为2,u,w向终点连流量为1

这样你会发现一定能满流??????啥证明啊

我们考虑建成二分图,然后就是左侧的点要满足点1经过黑白边到x->y的简单路径

然后y->x又要有一个边,这样才形成了一个奇环!

1   a

2 	b

3 	c

4 	d

即2->4可以构成奇环,1->2->4有黑白相交简单路径就好啦

考虑建立圆方树树,对于1->x->y

我们会有1->x'->x->y'->y

其中x',y'都是方点,x'->x->y'路径一定存在,但是1->x',y'->y可能有交

所以说我们还要求LCA来判断是不是有交集....

$O(mlogn)$

T5

考虑枚举了一维后,一个立方体的有限制的就是一个时间,即我们枚举时间扫过去的时候没有和这个立方体相交的那些时间

这个是线段树分治qwq,问题变成了二维的

如果只有二维,我们可以扫描线,本质上相当于我们枚举一维,然后另一维直接线段树维护这个区间交集

等等,区间交集?可以转换为每个点经过的区间数,这样所有经过n个得就是答案啦

二维限制取反,原本限制你会发现相当于一个十字形的区域求交

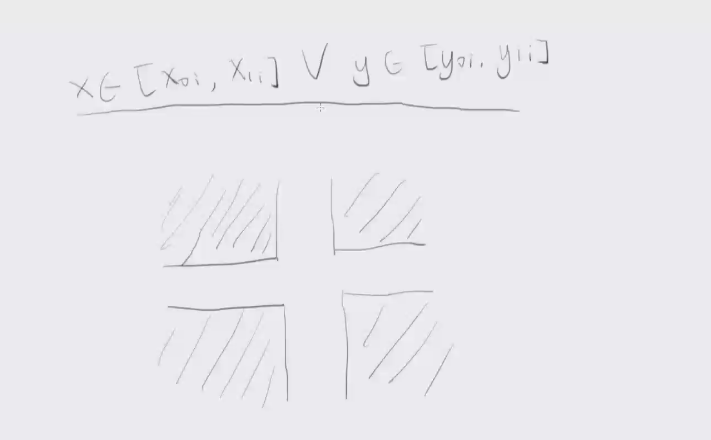
这个可以取反后变成四个矩形,然后问题也是四个矩形求并集看是不是全集

观察轮廓第一部分的相当于一个阶梯状上升的轮廓,右边又是一个阶梯下降的部分

难点在于有没有空隙,有就有解

考虑用一个线段树维护横坐标$[l,r]$上所有纵坐标的轮廓线是否存在

就是上轮廓的最大值下轮廓最小值以及这个区间是否存在解集

这个怎么判断呢?如果最大值小于最小值就无解,否则随便选择一个上传

合并的时候就是上轮廓最大值取max,下轮廓最小值取min

加入限制就相当于区间取min这样子

小米邀请赛

T6

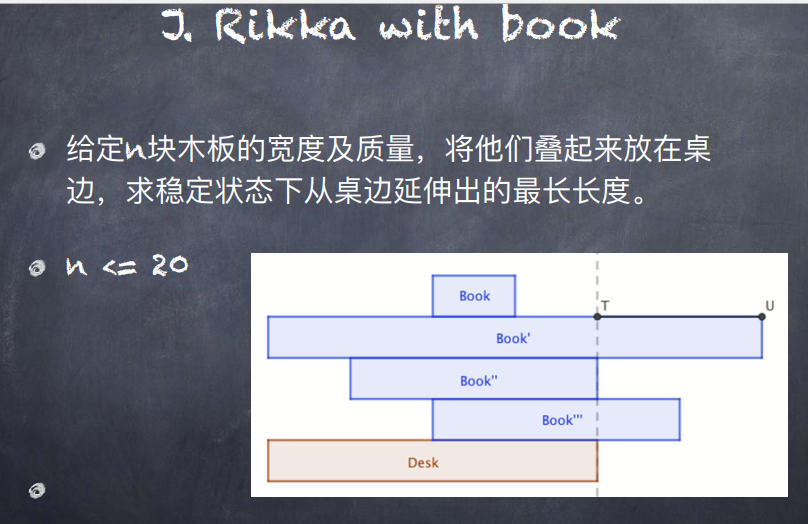
相当于重心的偏移量要尽可能大

显然每层的支撑面上重心都落在上面

也就是两层之间重心之差要尽可能最大

所以$dp_S$表示S集合内的木板已经放好了,然后最大的偏移量是什么

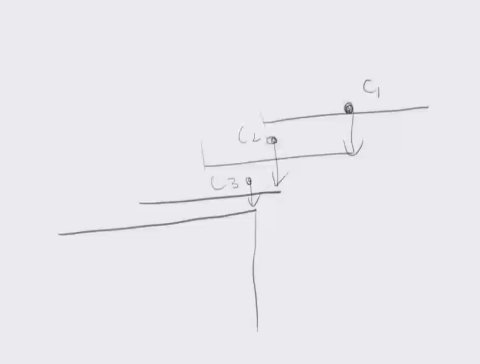
你考虑转移的时候考虑再塞进去一个木板,使得新木板和当前重心能够和在一起在桌子的最右端

你会发现我们这样能让重心稍稍右移qwq

计算重心右移按照重量加权处理,这可能也是只能dp的原因

T7

菊花图?

先都加进去

单独每个点两次操作就好了,因为移除/加入小点子树代价很小

毛毛虫图?

先把所有小点的答案处理出来,然后再处理毛毛虫的链上点的答案

一般图?

坏了,是栈,都萎了

对于菊花图,分治

solve(1,n)



add(mid+1,r),solve(l,m),del(m+1,r)



add(l,mid)solve(mid+1,r),del(l,mid)

一般图直接做不行,因为深度可以非常大

考虑重链剖分

我们先在处理一整个重链的答案,然后再去解决每颗重链上挂的小子树

同时小子树也可以剖分下去,这样我们就把所有点都达到了一遍

两个过程都是和节点个数有关,所以这里用启发式分裂,就是带权的分开整个重链或者每个子树qwq

n有$a_1~a_n$,我们就选择和最接近一半的弄上去

就是n分成两部分

两部分有很多小子树, $a_1,a_2,a_3...$

每个小子树再重复重链分成两部分

$T1(n)=T1(x)+T1(n-x)+n$

差不多$poly log$

T8

操作限制是每个x只能和相邻的数某个数交换一次

$x->x-1->x-2$

如果x和x-1交换过了,只有再撤回来一种操作方法,因为但凡移动只能让x离开x-1或者x-1离开x,而且不可能移动到其他地方....

也就是每个都是独立的,也就是说我们只需要考虑相邻的这个即可

加入我们已经确定了1~ x的考虑x+1~n的怎么交换

我们发现只需要考虑x,x+1这一个

$f(x,e)$表示x号点在e这条边进行了交换的方案数

你会发现我们只考虑x和x+1是否交换,因为如果x和x-1交换了,根据这个状态也能推得出来

然后根据这个状态来判断能否和x+1交换即可

T9

很像贪吃蛇,但是状态不好

相当于编号从小到大依次做决定是否屠龙,一旦决定一定会导致游戏结束

因为杀这个龙的人一定不会被杀,所以最多两轮

$(S,x)$表示当前龙的玩家为x

一个局面一个人当龙没有被杀掉就是所有杀掉他的人杀了他后都会被杀

$P(x)$为某个局面当龙的人是否没被杀$P(x)$为真当且仅当所有后继都是假的qwq,注意这个是有向步的,因为人数一定会减少

考虑朋友关系补图,然后一开始一个棋子放在x号点,然后依次移动不能经过之前的点直到自闭,判断这个可以带花树求最大匹配然后坏了

后手必胜当且仅当存在不包括x点的最大匹配

如果不存在,我们不可能走到一个未匹配点(否则有增广路了)

所以先手只要沿着匹配边走就一定能把后手逼到走投无路....

同时如果存在这样一个不包含x的最大匹配先手每一步都会走到一个最大匹配点上,否则我们就有增广路了....

然后后手每步再走匹配边即可qwq

但是你仔细发现这样我们要枚举一个点建图然后带花树冲匹配,坏了坏了$n^4$

建图好像就删掉一个点就好了

老师说这个可以加加速

就不会啦我直接疑惑啊

$\sum_{i=0}^{\infty}qwq$

那个题的做法很明确,就是我们先跑一遍最大流,如果S在残量网络能到达的点集大小+T在残量网络上能到达的点集大小之和等于n,我们就有唯一的最小割

反之,我们有一些不确定分入S还是T的点(两边都不连通),他们中的每一个连通块都可以任意分配

怎么刻画一个割是最小割啊qaq

$f(u,v)$表示u->v流量,我们要满足$f(v,u)=-f(u,v)$

c是最大流,$f(u,v)<=c(u,v)$

同时满足流量平衡限制,即流入总量等于流出总量

$\sum f_{s,u}=\sum {f_{u,t}}$

$S=V-s-t$

$\sum_{x\in S}\sum_{y \in V}f(x,y)=0$

拆开后有

$\sum_{x \in S} \sum_{y \in S}f(x,y)+\sum_{x \in S}f(x,S)+f(x,T)=0$

左边是0,右边移项即可,根据反对称性显然成立

这个定义是网络流的流量,记为x

那么我们总有对于一个包括源点不包括汇点的集合S,向一个集合S外的所有点流出的流量值为x

比较形象的理解是水流

证明:流量小于等于割量

因为有$f(x,y)<=c(x,y)$边权限制

所以有$\sum f(x,y)<=\sum c(x,y)$

这个等价于选一些边断开使得这个s->t不连通(广义割)

可以证明广义割集中的最小权值一定大于等于所有st割最小权值

最大流最小割定理:st最大流=st最小割

$r(u,v)=c(u,v)-f(u,v)$即残量网络

FF算法,延增广路一直增广.....这个东西啊复杂度和流量正相关qwq

考虑残量网络上s能到达的点集S,$T=V/S$

那么此时$c(s,t)=value(f)$,因为所有边流量都卡上上界c了!

此时一定满足最大流,最小割qwq

当然我们根据残量网络来证明也是可以的,就是对于所有$r(u,v)>0$

我们边都不在其中,而显然原图中$f(u,v)=c(u,v)$的$r(u,v)=0$!

所以根据这个我们可以看出是一个2-sat的条件,所以这个解集也就是2-sat的解集了!

怎么搞定他啊QAQ

首先在可能在判断就是看能不能钦定在其中然后达到最小割??

或者让(u,v)的权值减少一点,然后看是否存在r(u,v),如果不存在是否能够退流

或者2-sat:找是否存在u->v的增广路径

判断是否一定,增加eps检查最小割是否变大

2-sat: $u,v$为o标记,则可能不在,否则一定在

注意我们都是在残量上做的,就是说我们是在残量网络上跑2-sat去确定每个点的标记....

动 态 凸 包

我们不需要可持久化平衡树了

支持加入/删除,询问某个点处最大值

离线只有加=离线只有删

在线有的可以变成离线

$Graham$

按x轴排序,然后依次加点,总复杂度O(n),就是斜率优化维护凸包的过程

可 以 可 持 久 化

因为每次我们只是删除一个后缀

所以我们可以把凸壳的每个状态存在树上

然后考虑这个点加入能弹到哪里,这个可以二分

然后找到树上对应的那个祖先,搞一下就好了

这个可可持久化

平衡树版$Graham$

支持任意插入,不能删除

set维护所有凸壳

然后插入一个点,暴力向前找向后找弹出所有点

均摊是对的!

set找前驱后继可以使用$fingersearch$

实际上就是他的一个好的实现方式,我们只需要花费$siz+log$的复杂度实现查询siz次连续后继,即$it++$ qwq

手写线段树可以实现这个可持久化

但是还是不能支持删除:happy:

完全动态凸包

在线,不要求单调,可加可删,可持久化

可持久化平衡树是修改视为建立新的版本

然后非均摊复杂度的平衡树都很优秀qwq,建议使用本命平衡树$fhqtreap$

这个陈孙立版被yjz爷爷疯狂diss....

线段树实现

核心思想:每个点只维护跨过这个左右子树的边

叶子节点维护一个单独的点

非叶子节点维护这个凸壳信息然后钦定左子树的点集坐标小于右子树的(排序后建树)

假设我们已经求出左右的凸壳,合并后也一定是左边凸壳的前缀+中间边+右边的凸壳的后缀

$bridge(x)=(p(x),q(x))$非叶子节点维护这个边,p,q都是一个点

叶子节点维护$(a(x),a(x))$就是一个点的自环

那这个bridge是啥啊?

你会发现线段树的一个节点是这个区间的凸壳的克 鲁 斯 卡 尔 重 构 树 的代表边的点

怎么求:

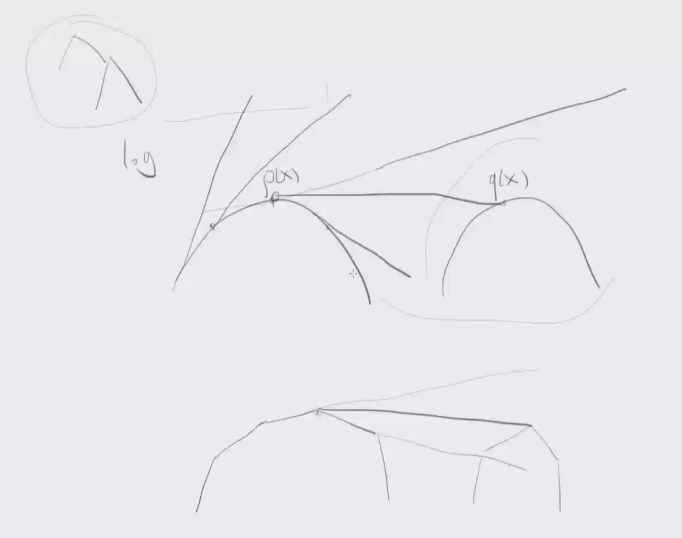
根据交点的范围,如果不在左边缩小右边直线范围,否则缩小左边直线范围,也就是说我们可以根据他的操作来考虑是不是左边区间被完全包含/需不需要递归左/右

实际运用上还是一个隐式凸壳的过程,dfs我们只dfs一边

注意我们求出bridge只需要花费虚树树高的代价就能解决,而这个,对于离线知道坐标范围可以线段树!

就是说我们只要知道哪些边在凸包上(隐式的凸包),然后根据这些边上我们二分就好了,二分每次都只会走向一个方向

而因为我们这样dfs代价只需要dfs到某两个叶子节点,所以这个合并算法的复杂度就是$Olog$的

单点修改只会影响一个点,$O(log^2n)$

区间询问只需要遍历到那个点之后用那个子树代表的隐式凸壳即可....

这个能查啥?

你发现我们可以花费log的复杂度建立出凸壳的虚树,然后支持不需要所有信息的一些操作

比如凸壳上二分!最简单的就是单点最大值查询!

关于这个O(d)棵子树,就是说一个向右的链,其所有左儿子构成的子树,这个子树数量显然是Od的

可持久化树结构

一个点x是由那些他指向的点代表的tree并成的!

我们最后维护的是一个类似DAG的东西,就是说每个点维护一个可持久化树

UOJ319

直接冲模板不行,俩log,即我们把k+1个不同的区间都凸包合并一下

我们可以考虑维护一个区间的前缀后缀的凸包信息然后合并,这样是$nlog^2n$

那么你会发现如果一个询问跨过了中间点,我们就直接用左边的后缀右边的前缀拼一下就好

接下来我们合并只需要一次而不是log次,所以是$O(mlogn+nlog^2n)$

而现在我们预处理一个区间的复杂度是加上了区间长度,所以是$O(nlog^2n)$的

如果一半直接继承儿子还能除个2的常数

这个不带修哈,是cdq分治维护凸包的基础

某个方向最远点是:$max(ax+by)$最小值我们维护下凸壳,最大值我们维护上凸壳

如果坐标单调而且单调加点单调删点,可以二进制分组,即只建立线段树一部分qwq

因为每次要合并两个集合,必然会让两个集合大小相同,而且大小之后翻倍,所以只会合并log次,就是$O(nlogn)$

删除也是一样,直接启发式分裂就好了,但是这个好像有问题!!就是我们可能加加删删每次都在濒临重构的边缘徘徊

所以我们可以随机增加一些乱数来防止复杂度退化qwq,就是说我们随机分组,变成$2^n+?$这样子

背包问题

求凑某个体积的是否可行,题解大小1e5,物品数量1e5

付公主的背包

01答案就是$\prod_{i=1}^n(1+x^{v_i})$

无穷答案就是$\prod_{i=1}^n (\frac{1}{1-x^{v_i}})$

这个连乘不太好,我们取ln

只看无穷答案

$ln(Q(x))=\sum_{i \in S}-ln(1-x^i)$

$ln(\frac{1}{x})=-\ln{x}$

这个直接移项就有了.....

然后再用$ln(1+x^a)=1+\frac{x^a}{1}+\frac{x^{2a}}{2}...$

这个是因为$ln(1+x)=1+\frac{x}{2}+\frac{x^2}{3}+\frac{x^3}{4}$

只询问一个体积的?二分用的次数k

相当于每个硬币多项式求和下然后自己卷一下$f^k(x)$

问一个值最少多少物品加出来?T为总体积

对于质量大于B的物品,我们最多用$T/B$次

$O(T/B)$次FFT计算一下使用T/B次物品的方案

然后在此基础上我们得到每个物品用大于的第一次凑出来的方案数

再在这个数组上做一个只使用小于B物品的DP即可

复杂度就是$O(T\sqrt T poly(log))$

如何快速在大DP数组上求出小物品?

优化(+,min)卷积上面是$[1,inf]$

A排序一下,相当于询问这个(i,j)转移到k的最小的$a_i$是什么

A分块一下,每块和B卷积,就能知道哪些位置可以凑出来

然后我们再把那些能的位置找到他具体是哪个A,这个复杂度是$O(T)$一次的

所以前面凑小物品复杂度是$O(T*B^{0.5})$

因为我们还要合并小大物品方案数的....所以用下面方法:

同时大物品方法不变,所以是$O(T*T/B)$

B取$T^{(2/3)}$最优就是$O(T^{4/3})$