夏晓光(loveJY)的博客

By 陈孙立

上午

说是简单题....啊这...

图论一般是树,仙人掌,DAG,有向图,无向图,网格图这样子的....

下面一般1e5级别

充要条件是小于号关系不成环

所以我们把图建出来然后缩点,考虑拓扑排序一下,能等于就等于这样子

会发现有点眼熟?之前好像我们也有一个限制某个点度数的题,但那道题要求最小生成树

所以我们只需要考虑跑出一个普通的生成树,然后如果s的度数太大了就暴力调整,就是说把一条横跨边换成树边....

这样我们好像也能对于t做一遍,当且仅当我们不用S的横跨边

这样不太对????

考虑s,t的边都不用,然后其他边构成一些连通块,他们可能与S有边,可能与t右边,可能与二者都有边

然后我们把只与s,t连边的连通块直接连边

剩下与s,t都有变的,如果超过原度数就无解,否则我们随便划分一下就做完了

如果这个带权了呢?

拟阵交..../jk

会发现我们贪心不一定是可以的....因为两个十进制数比较,位数长短是第一位的QAQ

所以我们可以考虑最短路,但是虽然位数长短是第一位的,我们高位还是要尽可能的低才行

所以我们可以优先走最小的那条边去更新,然后其他的还是dij,其实本质上我们是一个分层图....,然后一层一层的update

最后跑个回溯法输出路径即可

注意我们有0这种神仙边,会有前导0

从s开始只走权值为0的边能到那些点,然后merge这些点,再去做dij

就是长度和更新顺序两个排个序

我 抄 我 自 己

先搞一颗最小生成树

如果我们有解,能缩就缩,难道不行吗?

首先结论:$\sum{a}-\sum{b}>=0$,点权和大于等于边权和

充分性?因为一开始都是非负

考虑一棵树,如果有一个边能被缩就缩起来,而且一定存在一条边能被缩起来....

假设所有边都缩不了了....$a_u+a_v<len(u,v)$

那么$\sum{a_u*d_u}<\sum{len}$

显然左边那个大于$\sum{a}$

所以一定可以缩一下qwq

怎么维护啊QAQ

考虑DFS,然后对于点A,考虑$A+b_i+c_i$>=0,那么这棵子树一定能缩起来

然后A'成为这个新的权值,然后继续重复上面...

具体的我们有一个dfs函数(x,a)表示点x的子树得到权值a后缩起来的序列....

然后相当于按照$c_i-b_i$从大到小这样子缩,这样a非负了...

先dfs那棵最大的子树就好了Qwq这样我们保证每个阶段>=0了....

Part2匹配与网络流

Hall 定理

存在完美匹配的充要条件:

左半边的任何一个点的点集他小于等于与右半边的连边的点的点集

有上下界,先流了下界,边变成只有上界,再从超级源点向v连边流下界,再从u连边向超级汇点为下界,其实就是u点少了流量,而v点多了流量qwq

这样我们对于原来的源,我们从超级源点向源点inf,汇点向超级汇点inf

最大流再从s到t增广,否则反着来一下qwq

CF510E

首先显然的是我们如果把能成质数的一些东西连边能形成二分图,因为偶数之间奇数之间都不能连边...

然后考虑我们从这个图上找出环,那么我们从S向所以奇数点连流量为2的边,然后所有偶数点向T连流量为2的边

会发现我们从一个地方dfs一定能dfs出一个合法的环,否则无解

我切掉了

如果没有环长>=3就是个完美匹配了....

说人话,就是找出若干个环,使得每个点都被经过了一次QAQ

正则图一定有完美匹配,就是每个点度数都相等的图

所以我们先来个最小路径覆盖的模型

然后会发现每条边可能被用了两次

度数都是偶数??我们可以把一条边改成有向边u->v'保留,v->u'不要了

如果我们能定个向,使得新二分图能完美匹配就好了

定向?好像很熟悉??偶数且度数相同???

跑欧拉回路即可定向.......

国籍作业真强...

对于$a_i=a_j$,我们渴望[i+1,j]保留一下这本书,然后我们就能算出每本书保持的时间段

所以变成了一个书在一段时间内占领书架的位置并且剩下$c_i$的代价

相当于线段覆盖问题,然后每个位置不能覆盖超过k个,并且我们要最小化代价

直接上经典建图硬干即可qwq

保序回归问题

魔法商店

今年的版本:k=2而且一定要是整数....

k=1或者全是整数时

solve(S,low,high)表示确定S中的值都在low,high中

然后添加限制S集合中b的值只能在mid和mid+1中选择

然后取值是mid的向左区间递归,取值mid+1的在右区间递归

如果可能是实数,我们可以mid,mid+eps.....

缩个点,然后拓扑dp一下

可以用bitset优化连通性

先求出每个点作为正方形左上角时正方形最大的变成是多少,可以二分?

那么现在所有的点都要l(x,y)>=k

也就是说找到一条路径使得最小值最大

离线可以加点然后维护

在线可以把点权放到边权上然后最小生成树

变成求路径最小值...

....边双啊....

s,t位于同一边双里面你怎么定都是可以的啊...QAQ

然后对于不同边双的,我们还要考虑构成的边双树上那些树边会不会有冲突的情况....

这一部分我们可以打一个树上差分的标记啊Qwq,就能解决一条边是否会被双定向了...

下午

首先ans不会超过$O(n^3)$

而且我们会发现每个人走的时候都会减少1

可以考虑一个O(ans)的暴力

具体来说,如果一个点是有人的,就是周围最小值+1,否则是+0

然后我们发现某个点减少之后会使得周围四个点距离可能减少,而如果我们只bfs那些减少的,就可以O(ans)

GXOI2019旅行者

是不是做过啊?qwq

考虑二进制分组,然后我们每次以某一位为1的那些是起点,为0的那些是终点

不难发现只有log次bfs,而且我们对于一个作为答案的起点终点,一定会在某一位被算到,所以正确性也是有的qwq

还有一个做法,我们把所有关键点都是出发点

然后每个点记录一下最近关键点距离+从哪个关键点来?

然后对于一条边如果两个from不一样我们就可以计算答案Qwq

可能会有奇妙的原因丢失解....

所以我们可以把每个点记录两个from就可以了....就是两个从不同的起点的最短路,但是满足是全局最短和次短路....

好像直接暴力白边做LCT也是可以的!

然后我们考虑把所有白边都加进去,然后黑边加入组成生成树

然后考虑白边能扩大多少,对于一个黑边,他能管住一条路径上所有的白边

也就是说他们路径取min....

这个就可以数据结构维护了!LCT

然后我们就需要用取min的优势了,权值排序后从小到大加入,每个位置只会被取min一次,然后用一个并查集维护那些已经取min了的即可

暴力跳的时候就可以用并查集优化$O(nlogn)$

好选择题啊....

if(a==b)

正a->反b

我们能够翻转一些边方向

会发现每个出度<=1就不会有两个卡片违法了

考虑弱联通分量对于每个连通块,只有树或者基环树有解....

基环树的时候我们对于环上每个点下面是一个内向树就可以

对于基环树,除了环上边除外其他边只能内向,所以枚举正反向计算最少后,环方案是1||2

树的情况/jk内向树+?

根好像可以向下指一条链啊....QAQ不过这个应该也能处理

枚举根是什么,对于每个根看看多少条边需要翻转...这个显然可以树上递推或者换根DP

两边dfs

真网络流啊??

考虑一个数要被打开就要求两侧数和大于等于x

也就是流量和要为至少x

不会了

这个是线性规划的对偶??

建两排点

然后对于$a_i+b_j>=w$连边一个i,j,w

最后我们求一个完美匹配,对于所有在其中的边满足$a_i+b_j=w$

直接求二分图最大权匹配,这个东西就是答案....

1.对于任意匹配a->(i,j)->b,$\sum{a}+\sum{b}>=w$

2. km构造出了$\sum{a}+\sum{b}=\sum{w}$

我们可以想象成是一样的,然后不存在的边看成0

注意这个题求得是最大费用任意流,所以费用小于0的时候停止增广即可

L=14m,k=3

考虑dfs,1.未访问

2.已访问,已经退栈

3.已访问,未退栈

这样我们能得到一颗dfs树这样我们只会走4m-2n步

现在我们知道每个点出发能有返祖边

按照三进制一次确立每个点连向那个边,就是每访问一个返祖边就标记设为%3后的值

然后这样不断确定每一位

$log_3^n2m$

这样就还原了原图再最短路即可qwq

路径相邻颜色不同?带花树啊

然后做个毛线啊

必要条件,这个图存在欧拉回路,而且每个点相邻的边中不存在一种颜色出现次数超过一半,,,,

更具体的,我们不能存在一个点的某颜色度数超过一半

我们可以用欧拉回路对边定向,然后使得入度等于出度,并且不存在一个颜色入度超过一半

所以可以对每个入边分配一个出边,使得对于每个点他的颜色至少是交错的

然后会发现我们可能会有两个环交界处自闭

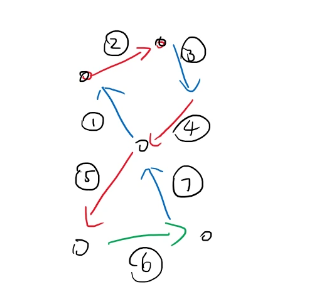
这时候我们就把下面那个环完全反过来qwq

而且要么反向要么不反向我们一定有一种方法使得这个成功

然后会发现一开始我们是构造出了几个相邻颜色不同的环,所以我们最后一定有解qwq

这个其实可以用双向链表来优化翻转过程,这样就是O(环)数来翻转

每个路径建一排点,每条边建一排点,如果路径包括了某个边我们就连一条边

限制就是花费1的代价标记一个点

如果这个点没有被标记,右边与之相连的点都要被标记

这个就是二分图最小点覆盖问题->最大匹配->最小割

问题在于可能有O(nm)条边

所以我们可以数据结构优化建图.....某个点向路径上所有点连边....

1.倍增优化建图

对于(x,l)新建一个点x,表示x及2^l级祖先的所有点

然后$(x,l)->(x,l-1),(x,l)->(f(x,l-1),l-1)$

这样子树上倍增的过程与之一样的,$O(nlogn+mlogn)$

当然也可以树链剖分优化建图

二分图:最小点覆盖=最大匹配=最小割

最大独立集=反图最小点覆盖

最小边覆盖->啊这大小差不多和匹配差不多

要么和匹配大小一样要么+起来是n

$a(i,j)=xa(1,1)+ya(1,j)+za(i,1)+w$

也就是确定了第一行第一列所有值就能推出其他所有的值...??这题怎么这么眼熟??

$y=(-1)^{i-1}$

$z=(-1)^{j-1}$

$w=(-1)^{i,j}$

所有我们先枚举$a_{1,1}$的取值

然后

$0<=ya(1,j)+za(i,1)+w<=1$

然后会发现无论怎么取值都可以用一个等价的2sat形式替换,这个可以手算一下

如果我们每个点度数大于2,那么我们选择那条父亲的边设置为1,之后就是直接暴力向哪个方向跳就好了

其实只要一开始降落在度数大于2的就能解决,之后走到度数为2的我们也只向上爬即可

问题就是一开始就是度数是2的怎么办啊??

最多我们可以向后走3步....

如果我们已知是一条链怎么办?

乱走3步也就是说我们会知道连续5条边

就是说如果我们知道连续5条边的染色方式就能知道链是正的还是反的

按照每6个一周期,010110的方式染色,这样任意连续五个都能知道方向了...

010110010110

就是算算本质不同的向前的和向后的所有子串有没有重复的qwq

这样整个题就构造完了.....

好像是输出任意两个点之间有多少条边!

首先随便搞一颗生成树,一定能构造出来的....否则无解

构造方法就是找度数为1的点和度数不为1的点连接

然后其他随便连一下就行了

不要求连通?

度数最大值要小于和的一半,而且度数和为偶数....

合并起来?

每个点选一些度数分配到生成树里面,另外的给到剩下的图

$d_i=\sum{2n-2}$

D_i-d_i<=\sumD_i-2n-2/2

其实就是$d_i$要大于等于什么东西

也就说每个d_i都有一个限制,然后总和还有个限制,随便构造即可

这样会T的,因为我们每次都选择最大值和次大值...

设k大值为$m_k$

$m_1,m_2,m_3$我们不断连$m_1$知道不满足那个条件

1.$m_1-k>(sum-2k)/2$

2.$m_1-k<3$

反正把$D_i$拍一下序然后二分一半

前面的一半连向后面的一半

每一段分别考虑复杂度线性