夏晓光(loveJY)的博客

ODE

n*n棋盘防止2n个车互不攻击方案数

EGF他

考虑我们一个炮相当于一个二分图上的一条边

然后不难发现,我们这张图有一些偶环

也就是说我们要统计n个点的二分图连乘偶环的方案数

先考虑只有一个环的EGF,不难发现一边一半,那么也就是说,如果我选择了三个点(左右都是)

那么按照排列拼起来的时候要除以2,同时因为我们是一个环,所以钦定左边编号最小的点作为开头,就要除以一个$\frac{1}{k}$

所以就是$\frac{x^i}{2i}$

二元EGF,左边选了若干个点右边选了若干个点,所以要处理$n!*n!$

因为说我们有两个参数QAQ

每次是两个东西合并,所以可重组合数要算两次,就要乘上两个$1/n!$

这个式子的生成函数是$-\frac{1}{2}(ln(1-x)+x)$

然后考虑这些卷起来就是exp起来,然后差不多就是这个形式

$\frac{1}{\sqrt{e^x(1-x)}}$

对于这个求导,然后有之前那个形式的东西,就有递推式了:

一个操作最多进行logn次,因为每次一定至少会让这个序列减半

期望就是骗人的了

$f_{i,j}$表示有多少长度为j的排列,满足操作i次后完蛋

考虑转移的时候枚举最大值的位置,假设是k吧

那么如果我中间要作为答案的最后一步,方案数是

$f_{i-1,k-1}*f_{i-1,n-k}$

否则就是放在左边或者右边完成这个过程,假如是左边,方案数是

$f_{i,k-1}*\sum_{j=0}^{i-1}f_{j,n-k}$

然后我们能写出$n^2logn$的递推式子了,然后他就不做人了

log次exp是要每次推一层的信息,一共log层

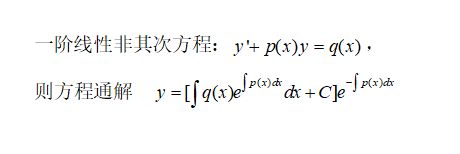
小羊说$Ce^x$肯定是解

我管他呢?不考就完了

考虑贡献,这个扯淡的转化就是选择三条在同一个路径上的边,如果两两不同,就会产生6倍的贡献,因为我们是有序的选择,$n!$

然后考虑两条边的时候,我们相当于先钦定两条边选择在不同上,然后剩下一个随便放,是$2*3=6$

这种转换其实类似于斯特林展开,就是$x^k$等价于x个盒子k个球往里面放

$x^3=\sum_{i=1}^3S(3,i)x^{3|}$

然后就是对于每一个i展开了,(选几个),那么一个就是1的贡献吧

然后根据组合意义这个是可以算出包含了某一个三条路径的或者两条路径这么一个方案数的

三条树选上的大概就是你想随意钦定一个边,然后两旁卷上选上一个边的树的方案数

然后两棵树一棵树更简单了

但是很扯淡的是,你想我们算贡献要乘上这个系数啊

去找老师问了一下,得到了一个离谱的答案

横戈跃马 16:50:48
哦，就大概选一条边的话，gf 是 F^2，然后 f(n)=n^n 这样

横戈跃马 16:51:15
哦然后选三条边是 F^4

16:51:58
不知道啊

横戈跃马 16:52:10
要是问一下我也不至于发个错的题解

一次方很好解释,就是那个方案数卷上权值*方案数即可

然后两棵树就是(方案数*权值)^2起来?

三棵树就是像他那样处理架空一条边吗?

rqy给出了对于一棵树的截然不同的构造方法,很不错的样子

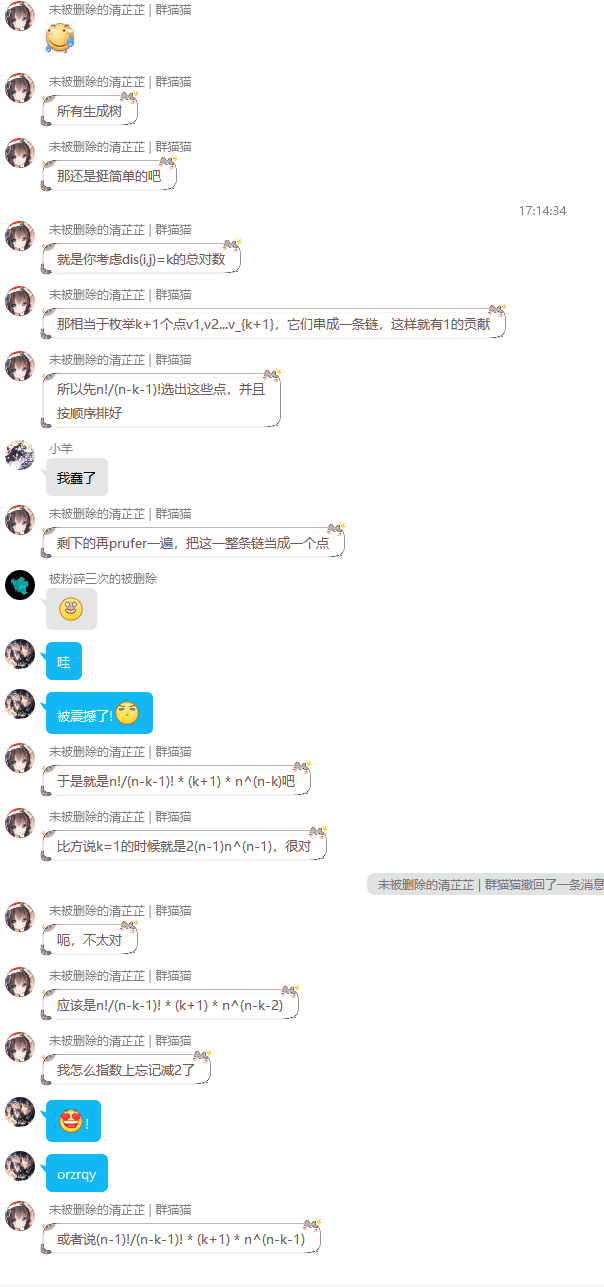
然鹅说这个东西很离谱,就是说我们要枚举这个权值所以很自闭,不能用作我们这个做法QAQ,其中最后一项应该是凯莱定理,就是要连通块一共有n-k个,然后n-k-2即可

森林,还是好好的按照我们这个方法卷积卷起来吧

答案的生成函数是$\sum_{i=0}^{\infty}x_i\sum_{j=1}^na^i_j$

这个东西考虑每一项弄出来然后求和,具体的,不难发现是

$\sum_{i=0}^{\infty} \frac{1}{1-a_ix}$

这个可以直接分治NTT,做法就是直接维护分子和分母

分子是$\sum_{i}\prod_{j!=i}\frac{1}{1-xa_i}$

分母是$\prod_{i}(1-xa_i)$

这个东西你会发现分母可以直接分治乘,到最后多项式直接就是$1-xa_i$

然后紧接着我们分治就是先拿左边的分子和右边的分母相乘,然后右边的分母和左边的分子相乘,得到新的分子

叶子的时候分子是1 qwq

还有多项式$\ln$做法很乐色

发现这个可以枚举$d_i$

钦定出现$d_i+1$次吧!因为我们再多项式中是出现$d_i$次的QAQ

$\prod_{i=1}^na_i^{d_i+1}(d_i+1)^m\sum_{i=1}^n(d_i+1)^m$

然后考虑prufer序列去限制度数,因为我们已经知道每个连通块的度数信息了,所以也不需要那么毒瘤了

$(n-2)!\prod a_i\sum_{\sum_{d_i}=n-2}\prod_{i=1}^n\frac{a_i^{d_i}}{(d_i)!}(d_i+1)^m\sum_{i=1}^n(d_i+1)^m$

注意那个$(d_i!)$是指这个可重

注意啊,我们这个$d_i$的限制要用生成函数搞掉

生成函数最大的优势就是他卷积起来选择的方案都可以体现,也就是说,虽然我们看上去做了一个npc的枚举,但实际上因为我们系数是乘起来的关系,所以可以生成函数去优化枚举过程----显然是用指数去优化

$A(x)=\sum_i \frac{x^i(i+1)^m}{i!}$

$B(x)=\sum_{i} \frac{x^i(i+1)^{2m}}{i!}$

注意这里我们没有把$a_i$乘入,所以考虑答案是

$\sum \frac{B(a_ix)}{A(a_ix)} \prod A(a_jx)$

$\sum \frac{B(a_ix)}{A(a_ix)}\exp \sum \ln A(a_jx)$

注意到我们左右无关了,所以只需要分别求出来然后乘起来就好了

现在有多项式$F_x$,我们要快速求$\sum_{i=1}^n F(a_ix)$

写开这个多项式,显然有

$f_0x+f_1*\sum{a_i} x+f_2*\sum {a_i}^2 x....$

这个就是我们之前说过的那个,可以使用分治NTT解决,

时间复杂度$O(nlog^2n)$

就是说如果i>j,我们乘上-1

然后发现我们直接平方就能得到那个$i!=j$了

$(\prod_{i<j}(a_j-a_i))^2*(-1)^{n*(n-1)/2}=\prod_{i!=j}(a_i-a_j)$

这尼玛的是多项式快速插值

然后

我选择死亡

艹,多 点 求 值

死亡选择我

n!划分为m个互不相同正整数相乘

互不相同很难,但是相同很简单,具体的,如果我们能容斥到至少0个组相同,就能解决一切了

先枚举一个划分的每一组大小,钦定这一组都选相同的!,然后考虑容斥系数就是$\prod{(a_i-1)}!(-1)^{a_i-1}$

你只需要考虑每种划分对于答案的贡献,只有那些所有的都只出现了1次的才会有1的系数贡献,其余的都是0啊

那你就考虑对于任意一个方案吗,方案数求法先对于n!分解质因数,然后相当于我们要做一个背包,每个质因数的指数都必须用$a_1...a_k$表示出来

注意现在为了方便我们现在钦定这m个数字本质不同,就是说他们无论怎么排列,都是不一样的,这样才能直接做背包啊,所以我们考虑一个划分情况对应了多少种实际方案?

首先有可重排列数,就是每个集合内部的元素无标号意义,然后有一个集合本质相同的除掉的排列数,就是说我大小为2的两个集合谁放在前面都没有关系

比如m=5,我们分为122,就是$\frac{5!}{1!2!2!*2}$

因为虽然现在每个元素都有标号了,我们本质相同的法则就变成了看上去不同

然后对于看上去不同,显然强制一样的一组内是一样的,然后选的个数相同的几组呢,他们如果有交换权值的次序,相当对应了$\frac{5!*different!}{k!}$,其中same是对于这k个东西背包的方案,他不同的值有哪几个,因为背包卷积的性质是自带一个可重组合数的,所以我们要对应上外面又双叒叕分配的编号(相当于编号两次),所以要额外除$k!$

注意到相当于最后还原到答案是要除$m!$,显然此时我们算的是m个正整数不同的方案qwq

很牛逼啊接下来这个东西...

给您1~m的值域限制,要求搞出n个互不相同的数乘起来,然后问总方案乘积之和

仔细思考会发现,此时一个大小为$a_i$的块对于答案的贡献是$(\sum {i^{a_i}})$

也就是说我们每个块的对于答案的贡献是独立的

同时,因为我们钦定的是编号,也就是说每个实际上是本质不同的!

上一次我们要除掉是因为多重背包手贱已经给我们多算了方案,而此时不需要再去除掉这个每个集合元素相同的多重组合数了!因为这个连乘是独立的也就是本来就是不同该多算的!

所以最后我们考虑exp

构建多项式$f_i=\sum \frac{(i-1)!(-1)^i(1^i+2^i+....+m^i)}{i!}x^i$

这个式子exp起来的第i项系数,就是我们有标号情况下的答案了