ZRDay7

强连通缩点

先dfs一遍,按照离开的顺序的到postorder

他的反序是dag上的拓扑序!

然后建立反向图

然后按照postorder正着枚举每一个点dfs,把每个点出发经过的所有点记录,他们就是一个强联通分量,就可以缩点

然后他就不做人了:

CF949C Data Center Maintenance

是相当于一个数组,然后对于位置x,y的值不能相同

那么如果 $u_x+1=u_y$ 就从x向y连一有向条边,表示x选了y就一定要选择

那么你就会发现,一个强联通分量中选择一个就要选择所有的QAQ

缩点

那么你就会发现这个就相当于选择最少的点,构成一个闭合子图

就是那些出度为0的分量中最小的点

妙啊!

2-SAT

两个变量,二元关系,~~多重酸爽体验!~~

3101. 「JSOI2019」精准预测

点为(n,T,0/1)

然后显然发现不需要nT个点,直接拿出关键点,然后关键点向未来时间连边就可

点数最多有O(m)了

然后缩点,如果有i为真到i为假,显然是不合法的,不过你会发现这个图一定是DAG不需要缩点,因为我们没有从假推向真的边啊

然后没有忽略的x,我们要求出答案,相当于找那些点能走出去得到多少个关键点 $(?,T+1,0)$

这个就是bitset优化传递闭包了,此时我们推出的信息应该是x为真哪些一定为假...

然后这样你会发现我们不知道弱不连通的两个点怎么办qwq

但是你会发现此时直接钦定这两个点为真,然后其他点为假,题目中的那个函数是一定成立的

所以就是可以的!

对于关键点分组,然后你会发现每次可以得到这些关键点的对于其他所有点的贡献

复杂度就是 $O(nB/64*n/B)$

欧拉回路

先判断连通!!!!

无向图是都是偶数

圈套圈算法

就是我们维护一个边的栈,然后每次dfs的时候先走未经过的边,如果这一整条边就走完了就自闭了(就是无路可走了),然后我们就把来到这个点的那条边加入栈中,最后dfs结束得到的从栈顶到栈底的就是正图的欧拉回路了

CF1361C Johnny and Megan's Necklace

枚举答案

就是说我们考虑 $2^k|(u xor v)$

这个条件可以枚举一个k,然后就是说两个点如果在 $mod 2^i$ 值是相同的,就是异或后整除的,就可以连一条边,然后就变成哈密尔顿路了?

然后你会发现我们可以对于这个条件可以转欧拉回路,具体的,我们对于原图的一条边(u,v)把 $(u\mod 2^i,v\mod 2^i)$ 两个点连边,然后在新图上的一个欧拉回路,就是经过了各个珍珠的中间边的形成的环的答案

可以二分,但是很无趣啊

割点割边

如果一个点出发走至多一条返祖边只能走到u,说明u是割点

同样的,如果一个点出发走至多一个返祖边只能走到dfn小于u的,说明u和他之间的是割边,因为如果是等于,还说明我们割掉不一定能走回去啊

其余的,对于根,如果他有多余一个儿子,也是割点

对于边双,特判这个父亲

点双边双

边双:

找到割边的时候

把得到的边弹出来即可

这些边的点集就是我们边双的点集

圆方树;

还是如果lowv==dfnu,就说明u是割点,要得出一个点双了,

直接取出所有栈里面的元素,然后注意了,此时的割点不弹出栈

最大值

有个结论:强联通分量无向之后一定是边双

证明就是你考虑一个割边,他无论怎么定向都只能保证从一侧的点集走到另一侧,不能走回去

这里好像边双严格定义就是没有割边的连通块哎qwq

所以我们就缩点后变成一颗树了,然后用LCT维护边双树就好了,也不需要啥圆方树维护点双了

然后直接单点修改然后链查询就好了

具体怎么维护呢?先split出来,然后把所有访问点x操作重定义为访问 $f_x$

将整颗splay的点x改成新点即可

然后access

广义圆方树

对于任意图都可以建立圆方树呢

就是将所有点双拉一个方点,然后点双内的所有点连边方点

此时树上两点必经之路就是圆方树上经过的点

UOJ

建立圆方树,然后直接用LCT维护链最小值信息

然后考虑直接做这个修改是 $O(邻居)$ 的

圆方树经典坑了,菊花图,所以我们不管哪个割点,只维护儿子信息,用set维护就能知道了

然后直接路径最小值

此时当LCA为方点的时候,还要加上方点父亲的的信息啊

Dinic

每次只增广到S距离差为1的边

就类似于每次增广最短路

这样就是 $O(n^2m)$ 了!

因为最短路最长 $O(m)$ ?

然后有当前弧优化

如果之前访问的增广完毕的点是无论如何没有必要再增广了

但是注意如果没有增广完毕,此时我们要直接break要不然当前弧优化就是假的!!

然后还有一个优化,就是y的所有出边都优化到底之后,要炸掉这个点,就是 $dis_y=-1$

能很快

zkw

就是我们把bfs改成spfa

每次沿着所有最短路径进行增广

注意我们这里就没有啥当前弧优化了

然后也要在反图上跑spfa哈

然后最后dfs增广

CF1082G Petya and Graph

考虑最小割

先拿到所有的收益

然后左边一排点表示边,右边一排点表示点

然后s向左边的点连接点权流量为s的然后右边点向T连接边权流量的边

然后最后我们一个边向两个点连边即可

跑Dinic即可得到最大流,角去就是答案

加势

三角不等式

$dis_x+c-dis_y\geq 0$

$c+dis_1-dis_2+c_2+dis_2-dis_3....$

抵消了

然后任意一条从S到T的路径,实际距离是新图上的距离再加上一个势函数 $dis_s-dis_t$

同时 $dis_s=0,-dis_t$ 就好了

这样的话每条边就是正权了

然后这一遍增广之后也要再把势能函数加上最短路值更新

第一遍如果负权边流量不是0就要跑spfa的\

https://community.topcoder.com/stat?c=problem_statement&pm=12432

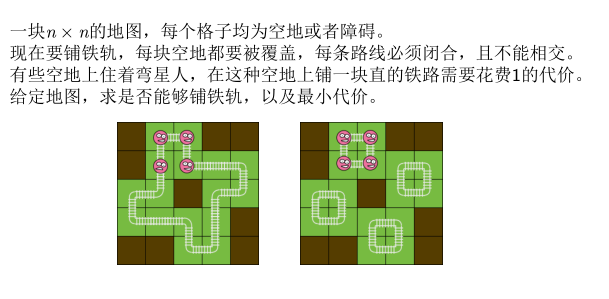
这个题就很magic啊

建模的出发点是一条一条方向确定,而不是一条条环确定啊

先黑白染色,那么每次我们只能从黑向白流啊

就是说我们每个点设置两个大方向上下/左右,然后再从大方向向小方向连边,其中左右和上下对应的第一个点要连费用为1的边,第二个点就要用费用为0的边,因为如果我们左右使用了,就一定会我们先从上下的走完了再走左右的!!

就是说s->1->上下

1->左右

上下-(0)>上

-(1)>下

左右-(0)>左

-(1)>右

之后小方向再向对应那个点的小方向连边即可,就是说s的右方向向t的左方向这样子

然后s向所有黑点连边,t向所有白点连边,这个流量为2,表示我可以延伸出两个插头

也就是说每次我们是贪心每个插头!!

又因为我们一定能够达到这个最大流,那么每个活动的点(有解情况下)一定能有两个插头连出去

同时跑最小费用,所以我们能尽可能的多选择一些点使他们处于拐弯,(充分利用左右)所以也能得到最优答案

上下界

流满下界

注意此时我们有的一定是

流出大于流入我们向T连边

流入大于流出的我们S向它连边

然后容量就是差值

如果新图能满流就平衡了

最大流

这个先流完下界

然后因为流量可以不平衡,我们原图中t向s连inf即可

然后求s到t的残量网络的最大流

最小流

一样的,从t到s流即可

CTT2020

竞赛图,问翻转某条边后强联通分量数

首先缩点,然后考虑不在一个强联通分量的边,翻转之后会使得这些缩点

那么会剪掉拓扑序之差个连通块

然后边界条件就是两个相邻的翻转,大概率是不变的

然后如果在一个强联通分量

求一个哈密尔顿回路

$mx_i$ 是不考虑这个环上的边,然后通过非环上的边能够走到的1到i位置中最大的编号的点是什么

然后我们有 $mx_x=x$ 的,x是这条边指向的点,就是翻转这条边新增的可能的连通块数

这个怎么O(n)维护呢?

你考虑我们每次把编号修改了,就是让环上第二个点变成第一个,然后每次暴力重新求每个点的mx,然后我们会发现最后一个点会变成n,也就是变大了,那么指向这个变大的点的mx会变大,直接修改这些点即可

实际上,我们就是在找每个点在不走他环上的父边的时候能走到的编号最大的点是什么qwq也就是那个low

怎么找哈密尔顿回路

考虑一个点去扩大环

因为是竞赛图,如果新点n和这个连通块存在多于一个入边和出边,就一定能找到一个三元环,然后扩展这个点!

怎么找这个新点?

考虑动态维护多个环,如果一些点x对于这个环全是入边,然后接着找到一些点y对于这个环都是出边

然后找到一个y到x有边的两个,他们两个可以缩成一个点,并入这个哈密尔顿路中

我们可以动态维护度数,说就是每个点和环上连了多少入边多少出边,在每次新加入一个点的时候显然是可以更新的,然后这样我们每次更新只需要扫一下每个点就能直接找到一个点或者两个点扩展加入了

P2304 [NOI2015] 小园丁与老司机

第一问是dp啊, $dp_i$ 表示第一次走到第i树所在的行经过的最大树木数

然后转移就是考虑我们每次一定是只能走这一行一段区间,所以可以先处理所有点向左走的,然后处理同一行所有点向右走的最大值,然后dp值就是取max

第二问就是有上下界的最小费用流

我们相当于把下界都流完然后每个点的入流和出流

如果出流多了s向这个连,否则这个向t连边,然后这样只需要从t向s跑一遍网络流实现最小流即可

https://community.topcoder.com/stat?c=problem_statement&pm=12500

L形骨牌铺建

网络流,只有黑点去匹配白点

昨天那个建图可以用来输出保证有解的方案QAQ

然后我们有更巧妙的建图

就是左边右边两排白点,表示奇数行/偶数行的白格,左边白点向S连,右边向T连然后中间两条黑点限制流量,然后一个白点向相邻最近排黑点连边即可

连通:

询问删掉每个点后,剩下编号相同的所有点的所有连通块数-1的和

建立圆方树,对于所以 $c_x=c_y$ 的点,他会对于路径上所有点产生一个贡献

然后我们就会发现这个问题很线段树合并,相当于查询,u子树中不同的儿子代表子树中编号为x的有多少个把

所以说我们可以在线段树合并的时候直接更新答案就是对于一个位置就是 $presum*siz$ 这样子

一个长度为n的数组,每次操作是把长度为l的连续段+-1

然后费用给定

希望最小费用使得整个数组单调不递减

显然差分...

然后我们有小于0的差分值s向他连边,然后大于0的向t连边

然后我们有对于一个区间加,相当于差分数组前面或者后面某个位置加减

就对应 $(x,x+l,inf,c)$ 或者 $(x+l,x,inf,c)$

然后1和n+1就直接特殊处理qaq

???不太懂的题->

左右都有n个点然后m个边

然后复制k次得到的图为 $f_k$

相邻的两排点有无穷大的边

我们要判断 $\lim_{k->\infty }F_k$ ,就是无限复制后的网络最大流

问题就是最大费用循环流,不循环一定去世了

容易发现,如果每个流量设置一的费用后,可以求最小费用最大流

然后我们就是要找一些环,使得长度总长最长

然后你考虑选若干的环,就是入度等于出度,就能保证构成环

对于每个点,拆成 $i$ 和 $i'$ ,然后我们新建源汇,边直接连边对应的两边的点,x到y'连边费用为-1

然后x向x'连边inf

然后根据网络流的最大流限制,你会发现每个点必须要是偶数

你考虑我们现在的费用流,如果s->x,x->t流量一定是n*inf

而如果 $x->x'$ 流量是inf-i,你就会发现x一定会向外面流了i,然后 $x'$ 接受了i

所以一定也是满流情况下尽可能多使用其他边啊

https://uoj.ac/problem/77

主席树优化建图

考虑我们最小割,每个点拆点,左边是代表黑点,右边代表白点

那么如果这个点选择黑色就向他之前满足条件的白点连接一个边啊

但是要拆点,就是拆出一个新点x表示这个东西,然后从u到这个点连接 $p_i$ 从这个点向v连接 $inf$

然后这个点要向所有满足条件的点连边

这些边显然可以用主席树优化建图

具体的就是建立1~i的值域线段树,然后我们每次加入i号点就用i代表的叶子向他连边即可,然后就变成了对于log个区间连边了

然后最小割整个问题,小心流量不能开小了