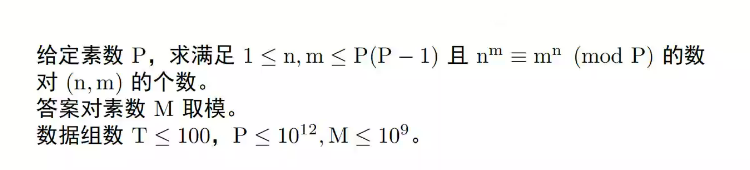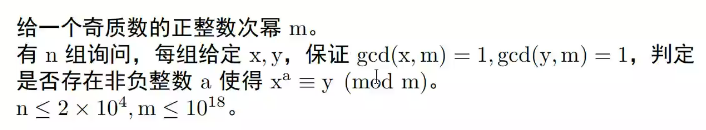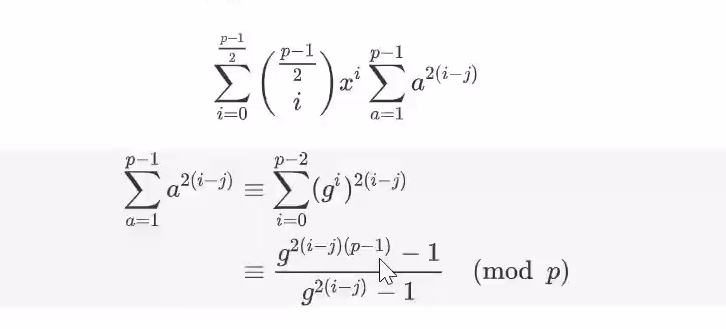夏晓光(loveJY)的博客

myh爷爷讲课!

excrt

线性同余方程组

满足

$ax+b \equiv c (\mod d)$

可以变成

$x\equiv a(\mod p)$

先变成

$ax\equiv b(\mod d)$

然后我们exgcd解出这个方程,假设最小正整数解为x',y'

$x = x_0+k*\frac{d}{(d,a)}$

$y=y_0+k*\frac{a}{(d,a)}$

如果$n_i$两两互质

然后我们就能发现所有在$\prod n_i$范围内的解就是唯一的

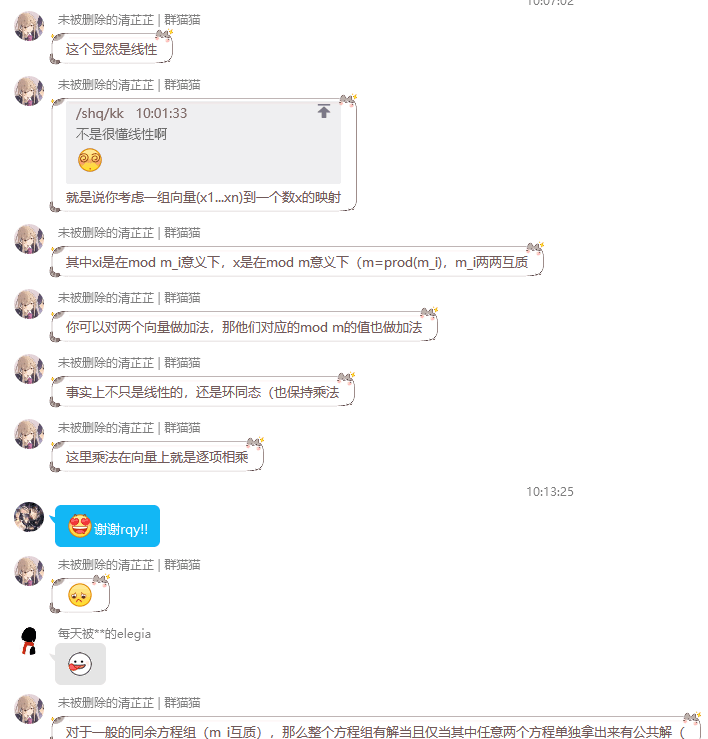
就有中国剩余定理

$e_i=(\prod_{j!=i}n_j)(mod \prod_i n_i)$

$x_0=\sum_{i=1}^n a_i e_i inv(e_i,n_i) (mod \prod_{i}n_i)$

因为当$\mod n_i$的时候,这个后面两项的乘积一定是1

然后我们得到的值就是$a_i$

其他项,他们的逆元*$e_i$因为互质一定是$n_i$的倍数,所以就是0

所有的解的形式就是

$x=x_0+\prod_{i=1}{n_i}*k$

不互质的时候可能会无解

excrt,数学归纳法

假设有$x_1,x_2$,他们满足这个方程组但是不同

首先我们此对于每个$n_i$模意义下都相同,但是对于$\prod p_i$不一定模意义相同

但是我们会发现$\mod LCM(p_1....p_n)$意义下一定不同

那么我们就可以去考虑怎么合并方程

$\begin{cases} x\equiv a_1 (mod n_1)\\ x\equiv a_2 (mod n_2)\\ \end{cases}$

$\begin{cases} x = a_1+y_1*n_1\\ x = a_2+y_2*n_2\\ \end{cases}$

然后我们考虑怎么搞搞

$n_1'y_1=n_2'y_2+(a_2'-a_1')$

$\mod n_2'$,然后除过去$n_1'$

$y_1=(a_2'-a_1)*inv(n_1',n_2')\mod n_2'$

屠龙勇士

大家都挺惨的

$\phi n=(p_i-1)\prod_{e_i}p_i^{e_i-1}$

这个$\phi n$代表的所有数构成了一个最大的乘法群

比如$\phi 12$代表了${1,5,7,11}$

他们的乘法运算结果$mod 12$都是自己

且均存在逆元,而且也都是自己

然后我们考虑原根

首先他要和模数互质,保证每次次方一定能得到一个不同的数

原根就是他的0次方到$\phi n-1$次方都是互不相同的

也就是构成了$\phi n$集合

其余互质的数,他们的次方也是一个完美的环,但是不一定大小为$\phi n$

然后我们会发现只有$2,4,p^k,2p^k$有原根

我们显然有$\phi \phi n$个原根,可以自己算一下

然后判定也不需要暴力,我们只需要找没有更小的循环节

这个好像只需要判断$\phi n$的因子是不是1就好了!

但是还是挺慢的

我们考虑所有因数,如果某一个是因子,那么他的约数随便划分一下,两个约数就一定都是1

就是$a^x=1,a^{xy}=1(\mod n)$

$x^{\phi n/p_k}\equiv 1(\mod n)$

直接判断即可qwq

然后我们构造最大循环群就很简单了

找到g,直接枚举一个x,所有$g^x$就是循环群

$e^x=y$

有

$x=\ln y$

怎么求x?

用这个方法乘法可以变成加法,然后求逆等价于乘-1,在$mod (\phi n)$

证明这个$\phi \phi n$个原根?

首先有一个g,然后我们$x=g^{f(x)}$

$f_g=1$

$0f(x),1f(x)....(\phi n-1)f(x)$互不相同?

所以$gcd(f(x),\phi n)=1$

phi的定义就整完了

整数mod n乘法群

mod 12

可以把mod 12中任意一个数变成$mod 4/mod 3$

因为12=4*3

考虑$5*7$是什么

然后我们有对应的坐标$(0,1),(1,0)(mod 3/mod 4)$

所以他们的乘法结果就是$(1,1)$

$phi 3=2,phi 4=2$

$7*11=(1,0)+(1,1)=(0,1)$

所以$7*11mod 12=5$

在mod 2^k意义下,5的阶是$2^{k-2}$

阶就是不断次方到第一个同余1的时候

然后我们会发现,对于mod 15,5的所有阶得到的结果,乘上-1这8个数就是$\phi 16$所有数

mod 2意义下和$\mod 2^{k-2}$意义下

1=(0,0)

5=(1,0)

9=(2,0)

13=(3,0)

$-1=(0,1)$

-5=(1,1)

阶

$gcd(a,n)=1$可以认为是一般有限群的拉格朗日定理推论

$a^{\phi(n)}=1$

$x^k=\equiv 1(mod n)$

然后最小的正整数k就是这个x的阶

怎么求阶呢?

和原根类似,就是直接考虑当前的阶设成$\phi n$

然后每次除掉一个质因子,看看是不是1,如果是则说明可以变得更下,继续做就好了qwq

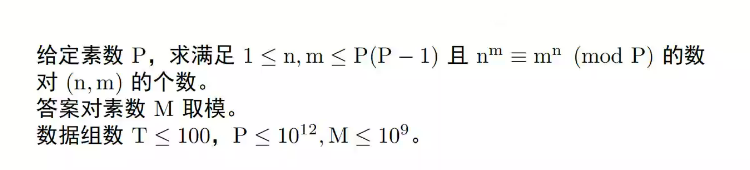
考虑变成

$\begin{cases} n&\equiv a(mod P) \\ n&\equiv b(mod P-1) \\ \end{cases}$

然后我们要有g吧?

然后$n\equiv g^a$

$(a,b)$

$(d,c)$

根据乘法群我们有

然后我们就有$ad\equiv cb (\mod P-1)$

$ad\equiv cb (\mod p^k)$

这个是整数mod n乘法群啊

所以abc都可以任意取,然后我们考虑d就是对应的逆元

答案就是$(\phi p^k)^3$

注意我们可能有更复杂的情况,如果abcd有

然后又是一道题

我们考虑怎么计算gcd

$gcd(x,\phi p^k)=gcd(x,p-1*(p^k-1))=gcd(x,p-1)*gcd(x,p^{k-1})$

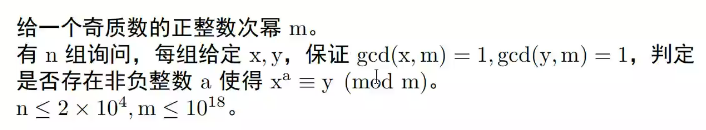
离散对数实质?

$gcd(f(x),\phi n)*ord(x)=\phi n$

这道题就需要满足$ord(x)|ord(y)$,观察一下就会有

$m=p^a$

而我们每次要求$\phi m$的质因数,所以要pollordrho分解

卢卡斯定理

$\binom{17}{6} \mod 5$

$\equiv \binom{3}{1}\binom{2}{1} \equiv 1 (\mod 5)$

就是p进制下每一位的组合数乘起来

库默尔定理

$V_P(n)$为n中素因子p出现次数

然后我们有???

不知道不重要

P不是质数,我们可以考虑把p分解,然后解决每个即可

首先我们需要excrt最后每个的结果

然后n!写成$p^{e1}q1,m!=p^{e1}q2,(n-m)!=p^{e3}q3$

显然三个e都是O(n)级别的

我们是可以对于q取模的啊,就是对于$p^k$取膜

所以就是$p^{e1-e2-e3}*(q1*(inv(q2,p^k)*inv(q3,p^k)))mod p^k$

怎么把n!写成这个形式呢?

预处理

$(d\equiv \prod_{i=0}^{p^k-1}i(gcd(i,p)=1))mod p^k$

有$n=17,p^k=4,17!=$

$1*3*5*7*9*11*17*2^8*(1*2*3*4*5*6*7*9)$

你会发现前面是d,就是d^4,然后乘上17,乘上$2^8$提出来,再递归右边部分

然后我们会发现这样只会进行$log_pn$轮qwq

二次剩余

素数p,然后整数x,看看是不是有$a^2\equiv x$

定义勒让德符号就是如果是二次剩余就是1,否则就是-1,如果p|a的话,就是0,也就是a可以大于p

然后有欧拉准则

$\frac{p}{a}\equiv a^{\frac{p-1}{2}}(\mod p)$

只有那个非二次剩余难证明

我们考虑所有ij=a,这样的对数,$i!=j$,同时又有p-1/2对所以这恰好就是$(p-1)!\equiv -1(\mod p)$

最后我们扩域之后得到的结果的bw中b一定是0

$x-x_0|x^2-a$

好像就是说有两个根,然后一定有一个是实数域的,然后另一个是复数域的

BSGS

这个可能平常是离散对数

实际上是求解$a^k=b$

a,b是代数结构里面的东西,ab是一个半群,就是能够做一个结合律就好了

$M=\lceil\sqrt |S|\rceil$

然后预处理前$a^m$,和$a^0,a^{m},a^{2m}...$

我们将后面的都插入哈希表

如果一个数出现了两次相同可能完蛋,就是我们两次都早的另一个点上去

,枚举一个q,小于m,查询$b*a^q$

如果找到的话$a^{cM}$,就有$b*a^q\equiv a^{cM}$

b有可能是$a^{cM-q}$,有逆元一定是

因为没有逆元就坏了,我们要带入检验,所以直接做就好了

二次互反律有了就能证明勒让德符号了

p,q都是奇质数

$\frac{p}{q}\frac{q}{p}=(-1)^{\frac{p-1}{2}*\frac{q-1}{2}}$

$\frac{a}{c}\frac{b}{c}=\frac{ab}{c}$

所以我们可以把什么分子倒过来继续递归之类的...

$\frac{5}{p}\frac{p}{5}=(-1)^{\frac{p-1}{2}*2}=1$

又因为乘式后面那个一定是1,然后前面也是1

所以我们就可以知道5有二次剩余

$\sqrt 5$

然后通项公式就有了,就有某一项的答案了

我们$\omega =\frac{1+\sqrt 5}{2}$

$-\frac{1}{w}=\frac{1-\sqrt 5}{2}$

$\omega ^n+\frac{(-1)^n}{w^n}=c$

然后我们试一下是1还是-1,然后我们解出$w^n$,二次方程求根就好了

再用一下bsgs就能找到这个n了吧?

就做完了

直接bsgs不行

我们有$2^{64}-1=(2^{32}-1)(2^{32}+1)$

这个直接bsgs就能过了

$p=p_1*p_2*p_3....$

$a^2+b^2\equiv x(\mod p)$

枚举一个a,然后就是看有多少个b

$\sum_{a=1}^{p-1}(\frac{x-a^2}{p})$

$\sum_{a=1}^{p-1}(x-a^2)^{\frac{p-1}{2}}(\mod p)$

你会发现-1和1的奇偶性不一样

这个怎么算呢?

二项式定理!

$\sum_{i=0}^{\frac{p-1}{2}}x^i\sum_{a=1}^{p-1}a^{2(\frac{p-i}{2}-i)}$

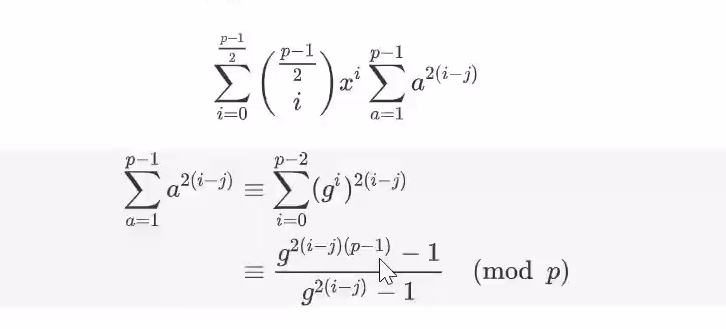
大型UB现场,j是哪来的?

所有这个j都是$\frac{p-1}{2}$第二歩是等比数列求和

$\frac{p-1}{2}-i=0 or \frac{p-1}{2}$

此时我们还有边界条件,首先0的情况只能是倍数很好知道

然后我们有1和-1的个数是一样的?

$f_1=1/0$

如果$f_1=0$

$f_n*f_1=f(1*n)=0$

常见积性函数

艾普西龙

当n=1时值为1,否则为0

容斥始祖

然后是约数个数函数,也是积性函数

$d_n=(e1+1)*(e2+1)*(e3+1)...$

约数和函数,也是积性函数

$d_1(n)=(1+p+...+p^{e_1})(1+p+....+p^{e_2})..$

可重质因子个数不是积性函数

$\lambda(n)=e_1+e_2+e_3...$

满足简单加法

$\lambda x+\lambda y=\lambda x+y$

然后有phi函数和莫比乌斯函数

都是反演基础了

狄利克雷卷积

网卡了没听qwq

$h_n=\sum_{d|n}f_dg_{n/d}$

贝尔级数

$F_z=\sum_{n>=1}\frac{f(n)}{n^z}$

这个多项式乘法就是f函数的狄利克雷卷积,为啥呢?

$f(z)G(z)=\sum_{n\geq 1}\frac{f(n_1)}{n_1^z}\sum_{m\geq 1}\frac{f(m_2)}{m_2^z}\\ =\sum \frac{f_dg_{n/d}}{n^z}$

这个就很阳间

对于一个积性函数我们只需要知道质数幂处的取值就能知道所有积性函数了

$F_p(z)=\sum f(p^z)z^i$

这个就是在质数幂处的贝尔级数

$l_p(z)=1+z+z^2....=\frac{1}{1-z}$

然后id函数呢?

$id^k_p(z)=1+p^k+p^{2k}+p^{3k}...=\frac{1}{1-p^kx}$

$\mu$ 函数呢?

$1-z$,因为剩下都是0

$\mu^2$,答案是$1+z$

$\phi(p)?$

$=1+p-1+p(p-1)+p^2(p-1)$

$=1+\frac{(p-1)z}{1-pz}$

$=\frac{1-z}{1-pz}$

也是很显然的

然后$\mu * 1 = 宇普西龙$的证明就是

$\frac{1}{1-z}*(1-z)$

$\phi_p z$卷1呢?

$\frac{1-z}{1-pz}*\frac{1}{(1-z)}$

显然了

积性函数求值

$\sum [p_k\leq n]=O(\frac{n}{\ln n})$

我们可能在质数的时候很快,但是在质数幂的时候很慢QAQ

而你会发现质数幂只有$ O(\frac{\sqrt n}{\ln n}) $

$\sum_{k>=2}\frac{k\sqrt{n}}{\ln n}$

然后假设我们对于一个k有$O(k^3)$才能求出

仍然可以!,因为我们这个所以复杂度还是$O(n)$的

$f=f*1*\mu$

然后阳间了起来呢!

$g_n=\sum_{d|n}f_d$

$f_n=\sum_{d|n}g_d\mu(\frac{n}{d})$

[l,h]选择有序n个数形成数组

然后问其中选择的数$gcd=k$的方案数

这个好像做过,再捋一遍思路吧

首先一定要除掉k,让gcd为1,否则我们不能保证选取两个数,然后让他们gcd至少小于$r-l+1$

然后就是变成$(\frac{r}{n}-\frac{l-1}{n})^n$

$\sum_{i=1}^n2^{f(i)}$

$2^{f(i)}=\sum_{d|n}\mu^2(d)$

有这个基本事实把/ll就是枚举哪些有没有啊sdsc讲过吧

然后我们考虑

$\sum_{d=1}^n\mu^2(d)\frac{n}{d}$

而$\mu^2(n)=\sum_{d^2|n}\mu(d)$

这个就很友好啊qwq

就是考虑容斥,出现一次或者0次的时候就是1,否则就是0

$=\sum_{d=1}^{\sqrt n}\mu(d) \lfloor\frac{n}{i^2}\rfloor$

$=\sum_{d=1}^{\sqrt n}\mu d (\sum_{j=1}^{\frac{n}{d^2}}d(j))$

这个积分就是$O(\sqrt nlogn)$

$\sum \sum \phi(ij)$

$d(nm)=\sum_{i|m}\sum_{j|n}[gcd(i,j)==1]$

$phi(ij)=phi(i)phi(j)gcd(i,j)/phi(gcd(i,j))$

这个生成方式就是考虑质因数展开式中i*j和phi i *phi j的差异就好了

显然要干掉p-1乘上p

也就是说我们只需要枚举一下gcd就好了

$\sum \sum \phi (ij)\\ \sum \sum \frac{\phi(i)\phi(j)gcd(i,j)}{\phi(gcd(i,j))}\\ \sum_{d=1}^{min(n,m)}\frac{d}{\phi(d)}\sum_{i=1}^{\frac{n}{d}}\sum_{j=1}^{\frac{m}{d}}\phi(id)\phi(jd)[(i,j)==1]\\ =\sum_{d=1}^{min(n,m)}\sum_{}$

myh咕了

杜教筛

我们要求f的前缀和

然后已经有了g,然后h*g很好求前缀和,g也是

$S_n=\sum f_i$

$\sum_{i=1}^ng(i)\sum_{j=1}{S(\frac{n}{i})}=\sum_{i=1}^nh(i)$

$S_n=\sum h_i-\sum_{i=2}^ng_iS(\frac{n}{i})$

然后直接数论分块

然后预处理前$n^{2/3}$的前缀和即可

我们的复杂度就是对对对的$O(n^{2/3})$

如果我们使用map实现记忆化有精彩的分析可以知道只有$O(\sqrt n logn+n^{2/3})$

嵌套杜教筛复杂度不变

只需要记忆化

简单分块

构造杜教筛可以用贝尔级数构造

首先$\mu \phi$可以直接构造

$f_n=n^k*\mu(n)$

我们使用n^k即可

$\sum_{d\mid n}\frac{n}{d}^kf_d=n^k\sum_{d|n}d^kd^{-k}\mu(n/d)=n^k[n==1]$

就做完了

$\sum \sum ijgcd(i,j)$

$\sum \sum ij\sum_{d|i,d|j}\phi d$

$\sum_{d=1}^nd^2\phi(d)(\sum^{\frac{n}{d}}i)^2$

如果有一些积性函数能在$\frac{n}{d}$处求出前缀和

那么我们有一些牛逼的积性函数的快速算法

$f_p=g_p$

然后$h=f/g,g=hg$

$\sum_{i=1}^{nf_i=\sum_{i=1}}n(\sum_{d|i}g(d)h(i/d)) $

$=\sum_{i=1}^nh(i)(\sum_{j=1}^{\frac{n}{i}}g_j)$

powerfulnumber是一个所有质因子指数都大于1的数

不难发现我们可以dfs找出所有powerfulnumber

所以每个质因子大于n的一定可以写成

$a^2b^3$

的形式,那么我们考虑有多少小于的等于他的,显然是$O(\sqrt n)$

而且远远跑不满

「LOJ #6053」简单的函数¶

$p ~xor~ c$

$f_p=p-1+2[p==2]$

就是一个多项式的形式啦

然后这个函数的幂次也能快速求值

比如-1,我们直接变为1,然后最后乘上-1

然后p就是直接做了

powerfulnumber

我们考虑把2的弄出来然后容掉就好了

$f_n=2^{\lambda(n)}$

问$S_n,n\leq 1e13$

$\mod 998244353$

这个没有实际意义吗?

$f_p=2$

$d_p=2$

然后我们可以用$O(\sqrt n)$

复杂度来算这个前缀和?

只对于powerfulnumbers算一遍复杂度很低的qaq

$\sum_{i=1}^{\sqrt n}\sum_{j=1}^{3\sqrt{\frac{n}{i^2}}}\sqrt{\frac{n}{i^2j^2}}$

然后我们这个东西就是$O(\sqrt n)$

Min25筛

对于更加一般化的积性函数求前缀和

$f_p$的形式能写成一个易于求积性函数的形式就好搞

就是完全积性函数的形式

比如$ap^2+bp+c$,我们只考虑p,p^2的和,最后乘上系数就好了

可以认为先求n/d处的f_p前缀和再去解决剩下的

$f_{prime^c}=g_{prime^c}$,但是$f_4$不一定为$g_4$

第一遍我们把2的倍数但不是质数删掉

然后再删3,继续这个过程

你会发现最小质因数一定小于等于$\sqrt n$

现在枚举了一个新的$p_j$,我们想要减去所有最小质因子为$p_j$且不是$p_j$

的数的贡献

那你会发现一定要大于等于$p_j^2$

$s_{i,j}=s_{i,j-1}-f_{p_j}*(s_{i/p_j,j-1}-s_{p_j-1,j-1})$

相当于我们减去最小质因子的贡献,所以我们有第一项

然后我们会多减去所以小于$p_j$的质数,就是后面那个,你发现只有质数会被统计入后面

然后怎么求出答案

这一部分是和powerfulnumber很像

getf就是根据这个质数来得到

然后答案的式子就和loj上那个式子一样直接模拟去算即可

有两种情况

第一是$p_i*c^k$,c的最小质因子对于p_i

第二部分是$p_i^c$

这个复杂度是$O(n^{1-\omega})$

在$n\leq 1e14$确实是对的,复杂度是$O(\frac{n^{3/4}}{\ln n})$

还能计算出所有$n/d$处的值啊

然后又是一个

我们删掉的数一定是类似$p_j^k*q$,所以这样的形式就能枚举

q的最小质因子是大于$p_j$的

$\sum_{i=1}^n\sum_{j|m!}d(i,j)=\sum_{i=1}^n\sum_{j|m!}\sum_{i'|i}\sum_{j'|j}[gcd(i',j')==1]\\ =\sum_{d=1}^n\mu(d)\sum_{i=1}^{n/d}d(i)\sum_{d|j',j|m!}1\\ =$

然后最后一个东西就是

$\prod_p\binom{v_p(m!)+1}{2}$

$v_p(m!)=\sum_{i\geq 1}\frac{m}{p^i}$

然后$v_p(m!)=\frac{m}{p!}(p>\sqrt m)$

然后就是有了,一个区间的质数个数

然后不学了